Estadística Correlacional
Inferencia, asociación y reporte
Sesión 4:
Inferencia 3: Intervalos de confianza
¿Preguntas de los textos?
¿Preguntas de los textos?
¿Dudas de la clase pasada?
Pilares de la inferencia
Curva normal
Error estándar
$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$
Diferencias desviación estándar y error estándar
Desviación estándar
\(\sigma=\sqrt{\frac{\Sigma(x_i-\bar{X})²}{N-1}}\)
Magnitud que expresa la dispersión en torno al promedio en la escala de la variable
Error estándar (del promedio)
$$\sigma_{\bar{X}}=SE=\frac{s}{\sqrt{N}}$$
Magnitud que equivale a la desviación estándar de los promedios de varias muestras
... y más de Error Estándar
- se calcula no solo para el promedio, sino para distintos estadísticos como correlación, regresión, desviación estándar (con distintas fórmulas para cada uno)
como está expresado en unidades estándar de variación, permite construir rangos de probabilidad basados enla distribución normal
estos rangos de probabilidad se conocen como intervalos de confianza
Intervalos de confianza
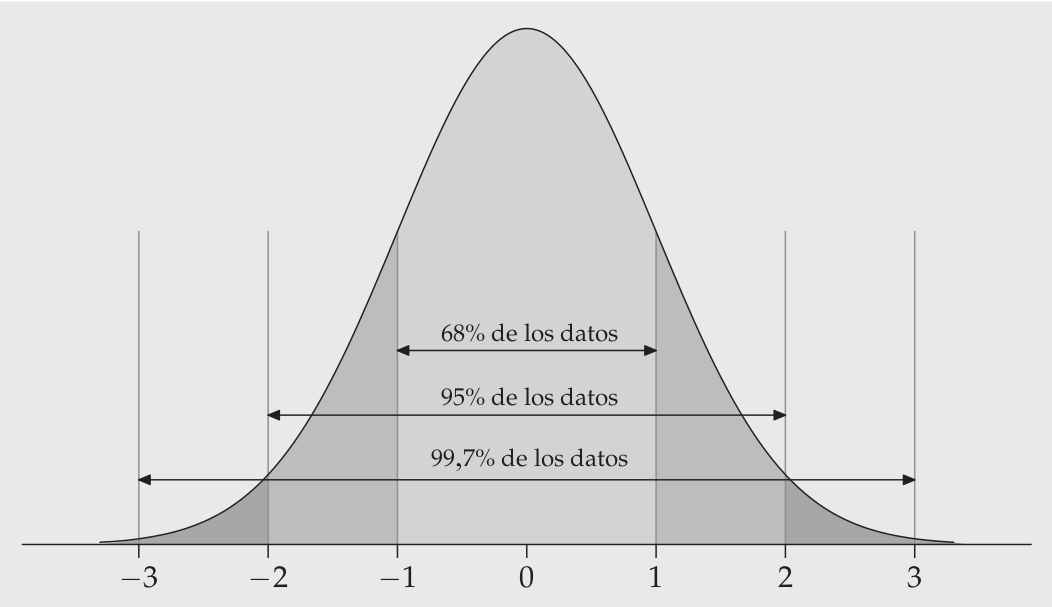
El error estándar, por su asociación a las áreas de la curva normal, se relaciona con niveles de probabilidad
Si sumo y resto error(es) estándar al promedio puedo construir un rango de valores probables en que se encuentra el parametro poblacional -> intervalo de confianza
- Por ejemplo, si tengo un promedio=10 y SE=1, puedo decir que aproximadamente el 68% de los casos se encuentran en el intervalo entre 9 y 11 (basado en distribución normal)
El error estándar, por su asociación a las áreas de la curva normal, se relaciona con niveles de probabilidad
Si sumo y resto error(es) estándar al promedio puedo construir un rango de valores probables en que se encuentra el parametro poblacional -> intervalo de confianza
- Por ejemplo, si tengo un promedio=10 y SE=1, puedo decir que aproximadamente el 68% de los casos se encuentran en el intervalo entre 9 y 11 (basado en distribución normal)
Pero ... ¿Es suficiente un rango que cubra al 68%
Error y confianza
- Un 68% implica que la probabilidad de que el promedio esté fuera de ese rango (o probabilidad de error) es de un 32% (100%-68%)
Error y confianza
- Un 68% implica que la probabilidad de que el promedio esté fuera de ese rango (o probabilidad de error) es de un 32% (100%-68%)
¿Es aceptable este nivel?
Error y confianza
- Un 68% implica que la probabilidad de que el promedio esté fuera de ese rango (o probabilidad de error) es de un 32% (100%-68%)
¿Es aceptable este nivel?
Esto es equivalente a preguntarse cuánto error estoy dispuesto a tolerar como resultado de una inferencia estadística
Error y confianza
- Un 68% implica que la probabilidad de que el promedio esté fuera de ese rango (o probabilidad de error) es de un 32% (100%-68%)
¿Es aceptable este nivel?
Esto es equivalente a preguntarse cuánto error estoy dispuesto a tolerar como resultado de una inferencia estadística
Y se asocia al concepto de nivel de confianza
¿Certeza o precisión?
No hay certezas, solo probabilidades
Las probabilidades se asocian a un rango (intervalo) que garantice un cierto nivel de confianza
¿Certeza o precisión?
No hay certezas, solo probabilidades
Las probabilidades se asocian a un rango (intervalo) que garantice un cierto nivel de confianza
Y esto requiere un compromiso o compensación (trade-off), ya que:
- un intervalo mayor poseerá un mayor nivel de confianza, pero en un rango de valores demasiado amplio
- un intervalo menor poseerá un menor nivel de confianza, pero en un rango de valores más estrecho
Es decir, qué tipo de conclusión prefiero:
el promedio de ingresos se encuentra entre 500.000 y 5.000.000, con un 99% de confianza, ó
el promedio de ingresos se encuentra entre 700.000 y 710.000, con un 65% de confianza
Es decir, qué tipo de conclusión prefiero:
el promedio de ingresos se encuentra entre 500.000 y 5.000.000, con un 99% de confianza, ó
el promedio de ingresos se encuentra entre 700.000 y 710.000, con un 65% de confianza
"con un 100% de probabilidad te aseguro que tu nota se encuentra entre 1 y 7"
Intervalos vs confianza
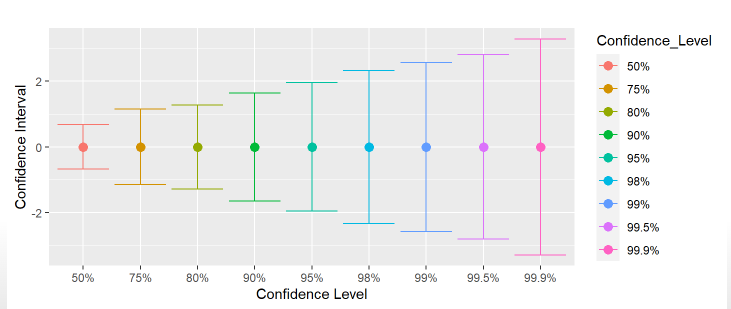
¿De qué depende el nivel de confianza?
en estadística inferencial, la confianza se asocia a 1 - probabilidad de error
la probabilidad de error a aceptar no es un criterio estadístico, es convencional
por convención, se acepta como estadísticamente significativa una probabilidad de error menor al 5%, lo que equivale (al menos) a un nivel de confianza del 95%
¿Qué significa un 95% de confianza?
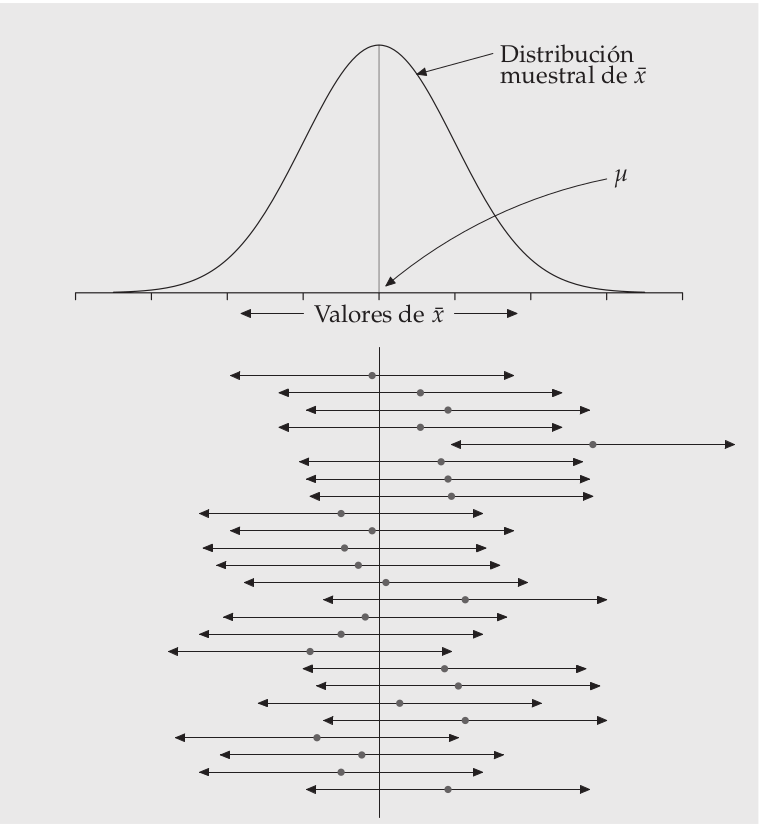
- que si tuviéramos la posibilidad de extraer múltiples muestras, el 95% de las veces nuestro intervalo contendría el promedio
¿Qué significa un 95% de confianza?
que si tuviéramos la posibilidad de extraer múltiples muestras, el 95% de las veces nuestro intervalo contendría el promedio
o que existe un 5% de probabilidad de error, es decir, de que el promedio de la muestra no sea el de la población
¿Qué significa un 95% de confianza?
que si tuviéramos la posibilidad de extraer múltiples muestras, el 95% de las veces nuestro intervalo contendría el promedio
o que existe un 5% de probabilidad de error, es decir, de que el promedio de la muestra no sea el de la población
o que las chances de error son 1 de 20
Un intervalo de confianza (IC o CI) es la mejor estimación del rango de un estadístico en la población (parámetro poblacional) con una muestra aleatoria
¿De qué depende el tamaño del intervalo de confianza?
¿Cómo se establece el nivel de confianza del intervalo?
¿De qué depende el tamaño del intervalo de confianza?
- recordemos que el intervalo de confianza se elabora sumando y restando errores estándar al promedio
$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$
¿De qué depende el tamaño del intervalo de confianza?
- recordemos que el intervalo de confianza se elabora sumando y restando errores estándar al promedio
$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$
dado que el tamaño muestral (N) se encuentra en el denominador del \(SE\), a mayor N, menor será el \(SE\) y menor el intervalo de confianza
esto tiene implicancias directas en el cálculo del tamaño muestral
Pasos en la construcción del intervalo de confianza (para un promedio)
Obtención de la media y el error estándar
Determinar el nivel de confianza (expresado en puntaje Z) para la construcción del intervalo
Aplicar fórmula:
$$\bar{X}\pm Z*\frac{\sigma}{\sqrt{N}}$$
Determinando el nivel de confianza
Nuestro promedio muestral \(\bar{x}\) posee una distribución normal con una desviación estandar = SE (error estándar)
Esto nos permite estimar probabilidades basados en los valores de la curva normal
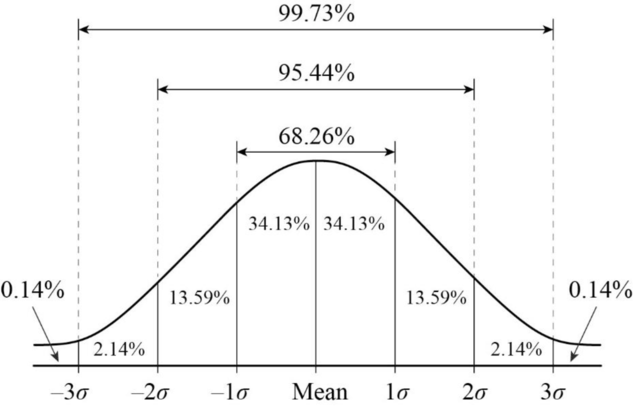
Valores del intervalo
Determinar el valor del límite superior y el límite inferior del intervalo en la curva normal para un nivel de confianza del 95%:
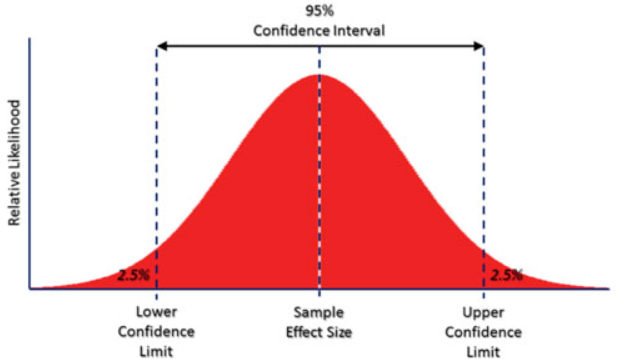
Valores del intervalo
El límite inferior de un intervalo al 95% de confianza corresponde al percentil 2,5%, y el límite superior al 97,5% (95% + 2,5%)

Y sabemos por la distribución normal que entre +/- 2 desviaciones estándar de la curva normal se encuentra el 95,44% de los casos:

Por lo tanto, para un 95% será algo menos que +/- 2ds ... pero cuánto específicamente?
De percentil a puntaje Z
Recordemos que al calcular el puntaje Z, el resultado se expresa en desviaciones estándar de la curva normal, lo que puede ser transformado a percentiles.
Por lo tanto, se puede hacer la operación inversa -> a que puntaje Z corresponde un determinado percentil
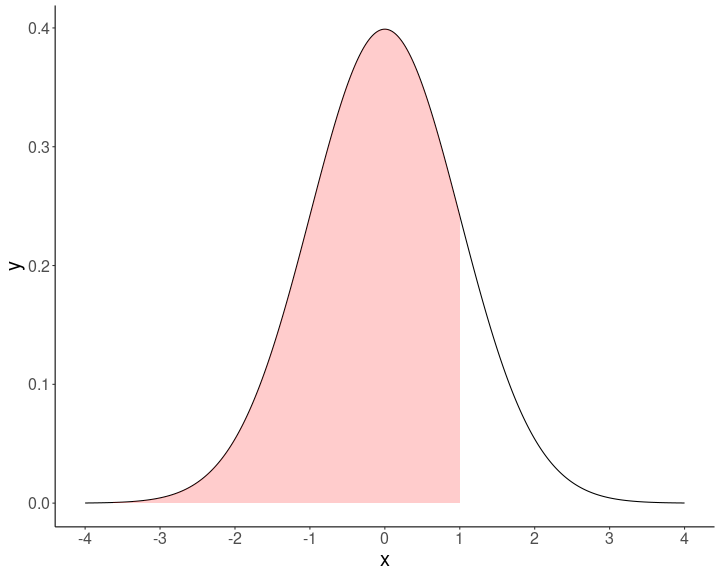
- Para hacer la equivalencia entre puntajes Z y percentiles vamos a una tabla de puntajes Z ... o directamente en R:
qnorm(0.025) # límite inferior[1] -1.959964qnorm(0.975) # límite superior[1] 1.959964Y aproximando: \(\pm{1.96}\). Por lo tanto:
Sumando y restando 1.96 errores estándar al promedio construimos un intervalo de confianza del 95%
Intervalo de 95% de confianza
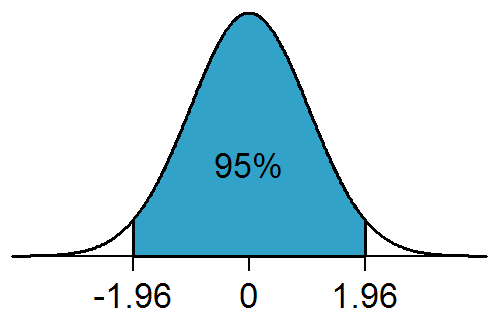
El valor de Z que deja el 2.5% de probabilidad en la cola izquierda y el 2.5% en la derecha es aproximadamente ±1.96
Un intervalo de confianza de \(\bar{x}\pm1.96SE\) abarca aproximadamente el 95% de los valores probables
En este caso, puedo decir que el promedio se encuentra en un rango de valores con un nivel de confianza de 95%
Ejemplo: intervalo de confianza para un promedio
Tenemos:
promedio de ingresos: 800.000
desviación estándar: 100.000
N muestral: 1.600
\begin{align*} SE&=\frac{s}{\sqrt{N}} \\\\ &=\frac{100.000}{\sqrt{1.600}} \\\\ &=\frac{100.000}{40}=2.500 \end{align*}
Tenemos: \(SE=2.500\), \(\bar{x}_{ingresos}=800.000\)
Con estos valores podemos construir un rango de probabilidad basado en la curva normal, sumando y restando errores estándar
\(\bar{X}{\color{red}\pm}1.96SE\) abarcan el 95% de los valores alrededor del promedio
- \(800.000 - (1.96*2.500) = 800.000 - 4.900={\color{red}{795.100}}\)
- \(800.000 + (1.96*2.500) = 800.000 + 4.900={\color{red}{804.900}}\)
Por lo tanto, podemos decir con un 95% de confianza que el promedio de ingresos se encuentra entre 795.100 y 804.900
Aumentando el nivel de confianza: 99%
además del 95% de confianza, otro nivel convencional es el 99% de confianza
con este nivel tenemos una menor probabildad de error, pero un intervalo más grande
en este caso, el límite inferior del intervalo es 0.5%, y el superior 99.5%
En R
Estimando valores Z para límites de intervalo de confianza al 99%:
qnorm(0.005) # límite inferior[1] -2.575829qnorm(0.995) # límite superior[1] 2.575829Generalizando:
Para un intervalo de confianza al 95%:
\(\bar{X}\pm1.96SE\)
Para un intervalo de confianza al 99%:
\(\bar{X}\pm2.58SE\)
Mismo ejemplo, pero al 99% de confianza
Tenemos:
promedio de ingresos: 800.000
desviación estándar: 100.000
N muestral: 1.600
\begin{align*} SE&=\frac{s}{\sqrt{N}} \\\\ &=\frac{100.000}{\sqrt{1.600}} \\\\ &=\frac{100.000}{40}=2.500 \end{align*}
Tenemos: \(SE=2.500\), \(\bar{x}_{ingresos}=800.000\)
\(\bar{X}{\color{red}\pm}2.58SE\) abarcan el 99% de los valores alrededor del promedio
- \(800.000 - (2.58*2.500) = 800.000 - 6.450={\color{red}{793.550}}\)
- \(800.000 + (2.58*2.500) = 800.000 + 6.450={\color{red}{806.450}}\)
Por lo tanto, podemos decir con un 99% de confianza que el promedio de ingresos se encuentra entre 793.550 y 806.450
Comparando intervalos:
95% de confianza: \(800.000\pm4.900=[795.100 - 804.900]\)
99% de confianza: \(800.000\pm6.450=[793.550 - 806.450]\)
Por lo tanto, a mayor nivel de confianza, mayor es el intervalo, pero disminuye la precisión o aumenta el margen de error
Margen de error
El margen de error es el valor en que puede oscilar el promedio en el intervalo.
Es decir, equivale a lo que se suma/resta al promedio para generar el intervalo, pero en general se expresa en términos de porcentaje
Ejemplo margen de error
- Para nuestro intervalo al 95%, el margen de error equivale a qué porcentaje es 4.900 en relación al total. Aplicando regla de 3 para porcentajes:
\(Margen-error_{95}=\frac{4.900*100}{800.000}=0.612\)
- Por lo tanto, el margen de error en este caso es de \(\pm{0.6}\%\)
Resumen
definición de intervalo de confianza
cálculo e interpretación del intervalo de confianza
comparación de intervalos con distinto nivel de confianza
margen de error
Estadística Correlacional
