Loading [MathJax]/jax/output/CommonHTML/fonts/TeX/fontdata.js
+ - 0:00:00
Notes for current slide
Notes for next slide

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Sesión 5:

Inferencia 4: Test de hipótesis

1 / 48

¿Qué hemos visto hasta ahora?

... y ¿para qué?

2 / 48

3 / 48

¿Qué puedo decir de la población a partir de mi muestra?

4 / 48

¿Qué puedo decir de la población a partir de mi muestra?

PROBABILIDADES ... de un rango de valores

4 / 48

¿Qué puedo decir de la población a partir de mi muestra?

PROBABILIDADES ... de un rango de valores

¿Cómo llego al rango de valores probables de un parámetro poblacional obtenido a partir de una muestra?

4 / 48

Probabilidades

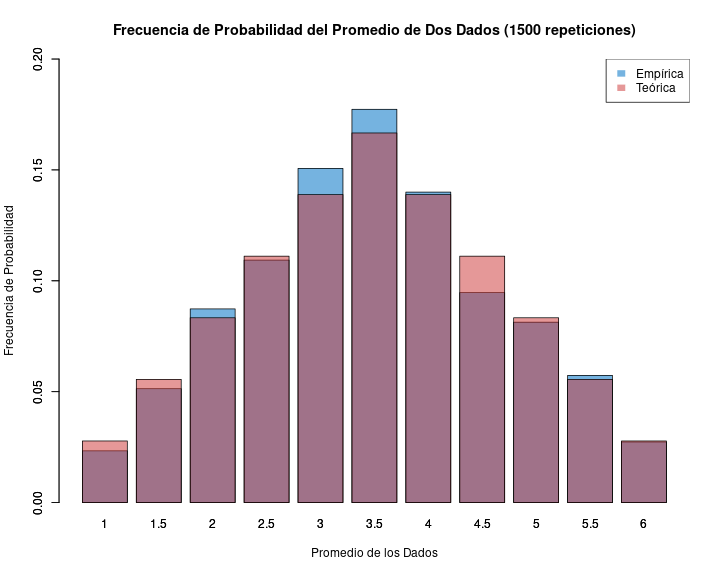
  • Podemos calcular probabilidades basados en una distribución teórica de ocurrencia de eventos.

  • Ej: En teoría, la probabilidad de que salga sello al tirar una moneda es 50%

  • Mientras más repetimos el evento, más se van a acercar los resultados (distribución empírica) a la probabilidad del evento (distribución teórica)


5 / 48

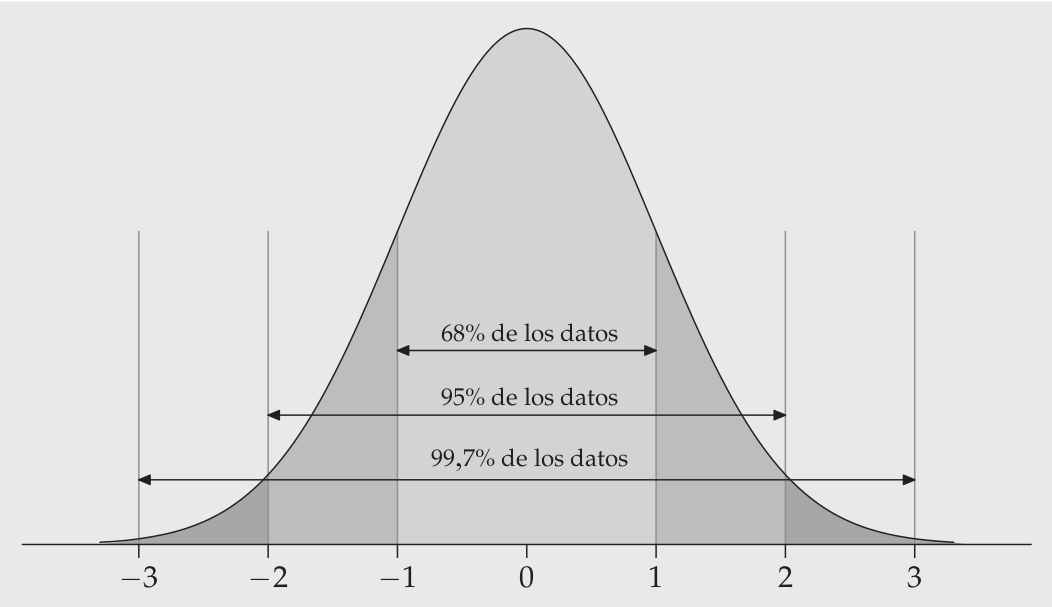
Curva Normal

  • Hay una serie de eventos que en términos teóricos y empíricos tienen una distribución particular en torno al valor central -> normal

  • La curva normal es una distribución teórica que nos permite tener un estándar con el cual comparar distribuciones empíricas




6 / 48

Teorema del límite central y error estándar

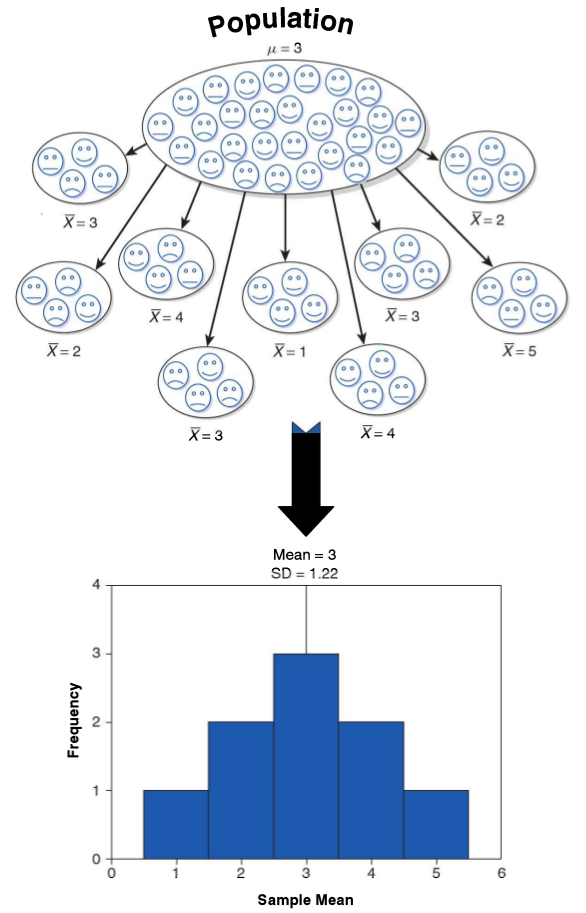
  • si pudiera calcular un estadístico en muchas muestras distintas (ej: promedio) este se distribuiría de manera normal

  • el error estándar es la formula que nos permite obtener el valor de la desviación estándar de los promedios con una sola muestra


σˉX=s√N

7 / 48

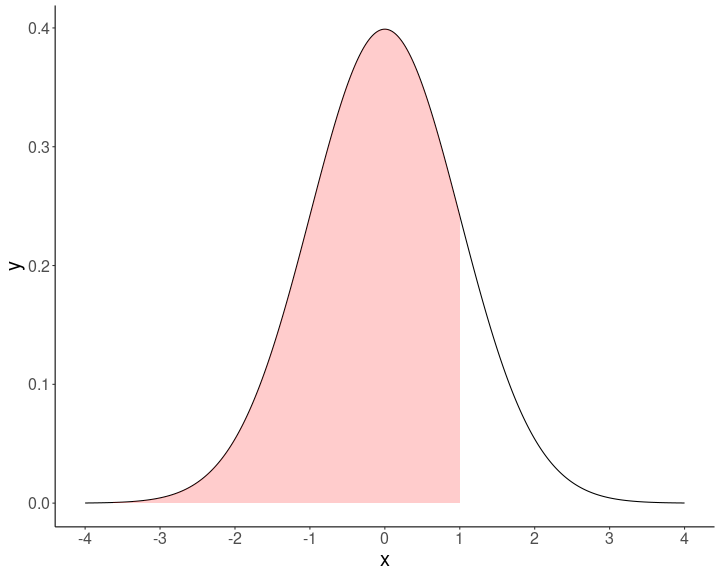
Puntajes Z

  • el puntaje Z es una medida de distancias del promedio en una distribución normal, que tiene promedio 0 y desviación estándar 1

  • Z expresa cualquier puntaje en desviaciones estándar desde el promedio (de la curva normal)

  • Z permite además obtener el valor del percentil de cada puntaje

z=x−μσ

8 / 48

Intervalos de confianza [para el promedio]

  • rango de probabilidad del valor de un parámetro en la población

  • Para construirlo, 4 pasos:

    1- establecer nivel de confianza (convencionalmente 95%)

    2- definir puntaje Z correspondiente a este intervalo (para 95% es 1.96)

9 / 48

Intervalos de confianza [para el promedio]

  • rango de probabilidad del valor de un parámetro en la población

  • Para construirlo, 4 pasos:

    1- establecer nivel de confianza (convencionalmente 95%)

    2- definir puntaje Z correspondiente a este intervalo (para 95% es 1.96)

3- multiplicar Z por el error estándar

4 - restar al promedio (límite inferior) y sumar (límite superior)

ˉX±Z∗σ√N

9 / 48

10 / 48


¿Qué es una hipótesis?

11 / 48


¿Qué es una hipótesis?

¿Cuándo una hipótesis es verdadera?

11 / 48

Una hipótesis es una aseveración o una predicción que se desprende de una teoría sobre una situación que ocurre en la población en estudio

12 / 48

¿Cuándo se puede verificar una hipótesis?

13 / 48

¿Cuándo se puede verificar una hipótesis?

-> NUNCA

13 / 48

¿Cuándo se puede verificar una hipótesis?

-> NUNCA

... pero, se puede falsar

13 / 48

Popper y la falsabilidad

"el criterio de demarcación que hemos de adoptar no es el de la verificabilidad, sino el de la falsabilidad de los sistemas. Dicho de otro modo: no exigiré que un sistema científico pueda ser seleccionado, de una vez para siempre, en un sentido positivo; pero sí que sea susceptible de selección en un sentido negativo por medio de contrastes o pruebas empíricas: ha de ser posible refutar por la experiencia un sistema científico empírico" (Popper, 1982, p. 40)

14 / 48

Contraste de hipótesis y falsación

  • El verificar una hipótesis no hace que una teoría sea verdadera

  • Se puede intentar refutar una teoría (falsarla) mediante un contraejemplo o hipótesis contraria

  • Si no es posible refutar la hipótesis contraria, entonces la teoría queda aceptada provisionalmente

15 / 48

Ejemplo

Teoría: todos los cuervos son negros

Hipótesis de verificación: hay cuervos negros

Hipótesis de falsación: hay cuervos blancos


16 / 48

Lógica de contraste de hipótesis:

Intentar falsear lo que es contrario a nuestra hipótesis original

17 / 48

Lógica de contraste de hipótesis:

Intentar falsear lo que es contrario a nuestra hipótesis original

En estadística, esta "hipótesis contraria" se denomina la HIPÓTESIS NULA

17 / 48

buscamos RECHAZAR LA HIPÓTESIS NULA

si logramos rechazar la hipótesis nula (o sea, que lo contrario de nuestra teoría no es verdad), entonces encontramos evidencia a favor de nuestra teoría

Buscamos no encontrar cuervos blancos

18 / 48

19 / 48

Tipos de hipótesis

  • Según número de variables involucradas: univariadas, bivariadas, multivariadas

  • Según tipo de contraste

    • hipótesis de diferencia (distinto de)

    • hipótesis de comparación (mayor/menor qué)

-> más detalle de tipos de hipótesis prox. clase, ahora vamos a un ejemplo

20 / 48

¿Existen diferencias salariales entre hombres y mujeres en Chile?

Hipótesis general Hipótesis estadística
Existen diferencias salariales entre hombres y mujeres Hipótesis alternativa: Las diferencias son distintas de cero
No existen diferencias salariales entre hombres y mujeres Hipótesis nula: Las diferencias no son distintas de cero
21 / 48

Cuestionario CASEN

22 / 48

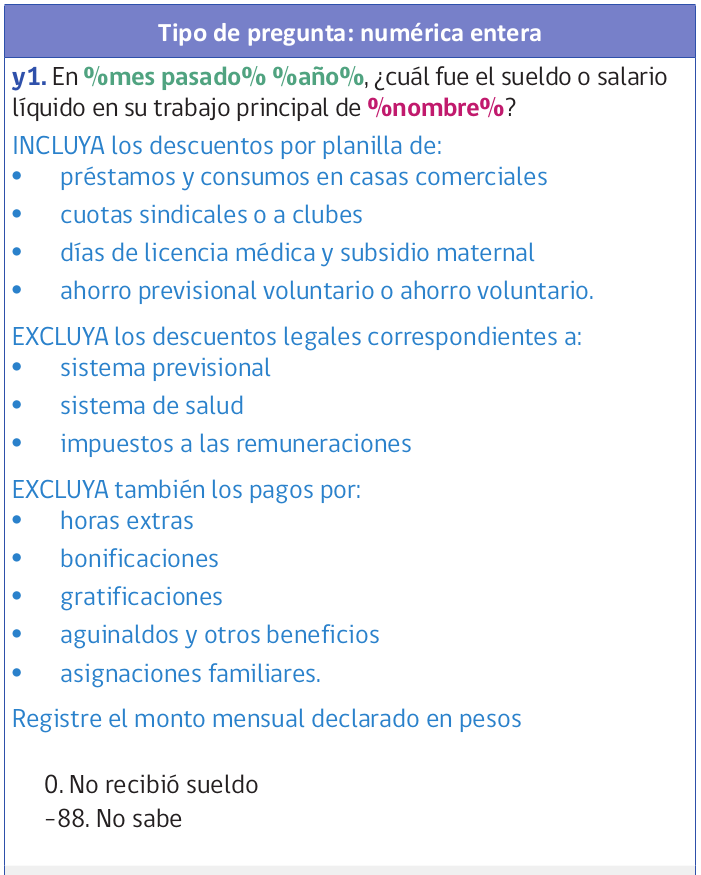
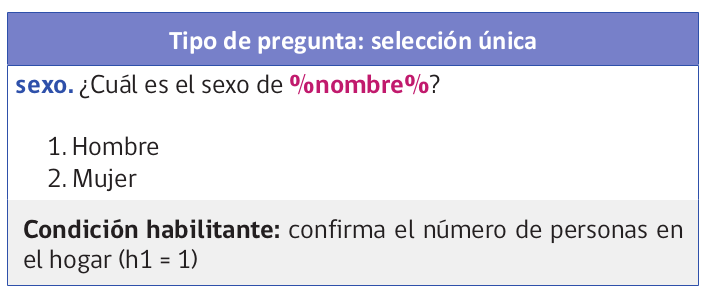
Datos CASEN 2022

Vamos a generar una submuestra de 350 casos de CASEN para ilustrar de mejor manera el sentido del test de hipótesis

pacman::p_load(sjmisc, haven, dplyr, stargazer, interpretCI, kableExtra)
load("casen2022_inf2.Rdata")
options(scipen=999) # para evitar notación en los ceros
set.seed(20) # para fijar el resultado aleatorio
casen_350 <- casen2022_inf %>% select(salario,sexo)  %>% sample_n(350)
casen_350 <- na.omit(casen_350)
23 / 48

Datos

stargazer(as.data.frame(casen_350), type = "text")
======================================================
Statistic  N     Mean      St. Dev.    Min      Max   
------------------------------------------------------
salario   343 634,402.300 459,180.200 30,000 2,900,000
sexo      343    1.402       0.491      1        2    
------------------------------------------------------
24 / 48
casen_350%>% # se especifica la base de datos
   dplyr::group_by(sexo=sjlabelled::as_label(sexo)) %>% # se agrupan por la variable categórica y se usan sus etiquetas con as_label
  dplyr::summarise(Obs.=n(),Promedio=mean(salario, na.rm=TRUE),SD=sd(salario, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla
  kable(, format = "markdown") # se genera la tabla
sexo Obs. Promedio SD
1. Hombre 205 654585.4 468692.5
2. Mujer 138 604420.3 444666.0

Diferencia salarial = 654.585-604.420=50.165

25 / 48

Procedimiento: 5 pasos de la inferencia (ajustados de Ritchey)

  1. Formular hipótesis ( H0 y HA)

  2. Obtener error estándar y estadístico de prueba empírico correspondiente (ej: Z o t)

  3. Establecer la probabilidad de error α (usualmente 0.05) y obtener valor crítico (teórico) de la prueba correspondiente

  4. Cálculo de intervalo de confianza / contraste valores empírico/crítico

  5. Interpretación

26 / 48

1. Formular hipótesis

Contrastamos la hipótesis nula (no hay diferencias de promedios entre grupos):

H0:ˉXhombres−ˉXmujeres=0

En referencia a la siguiente hipótesis alternativa:

Ha:ˉXhombres−ˉXmujeres≠0

27 / 48

(2. Error estándar y estadístico de prueba)

  • (Una nota preliminar) En general, existen 2 formas de realizar el contraste de hipótesis:

    • intervalo de confianza, asociado al error estándar
    • contraste con valor crítico, asociado al estadístico de prueba

  • Ambos entregan información consistente y complementaria

  • En esta clase vamos a estimar solo el intervalo, la próxima veremos el contraste con valor crítico, que el caso de diferencia de medias corresponde a la prueba t de student.

28 / 48

2. Error estándar (y estadístico de prueba)

  • Cada estadístico tiene su propia fórmula de error estándar

  • En el caso de la diferencia de medias (en este caso, de hombres y mujeres), el error estándar es:

SE=√σdiffna+σdiffnb Donde

σdiff=σ2a(na−1)+σ2b(nb−1)na+nb−2

  • como se puede apreciar, es una extensión del error estandar del promedio pero para dos grupos distintos
29 / 48

Cálculo de la desviación estándar de las diferencias de promedios:

σdiff=4686922(205−1)+4446662(138−1)205+138−2=44813126936256+27088715663172341=210855843400

30 / 48

Y enfonces el error estándar de la diferencia de medias: SE=√σdiffna+σdiffnb=√210855843400205+210855843400138=50561

31 / 48

3. Establecer probabilidad de error

  • asumimos que existe una probabilidad de error al rechazar H0, para lo cual fijamos un límite convencional -> usualmente un 5%

  • ¿error de qué? -> de rechazar H0 cuando esta existe en la población.

  • Esto se conoce como la probabilidad de error Tipo I o α (alfa)
32 / 48

Hipotesis nula ( H0) y tipos de error

33 / 48

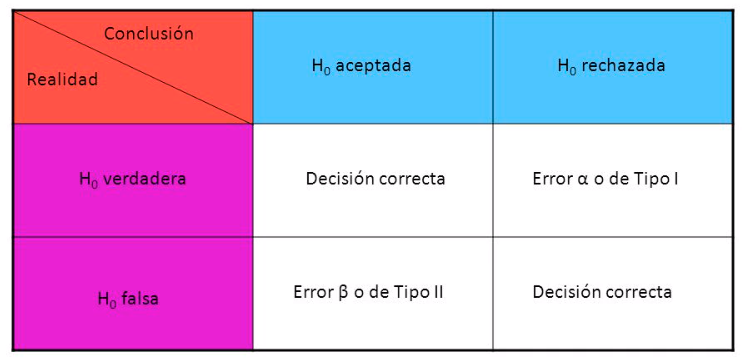
En nuestro ejemplo:

H0:ˉXsueldo mujeres−ˉXsueldo hombres=0

  • Si hay diferencias de sueldo en la población y rechazamos H0: decisión correcta

  • Si no hay diferencias de sueldo en la población y rechazamos H0: Error tipo I

El Error Tipo I equivale a encontrar cosas en nuestra muestra que no existen en la población

34 / 48

Hipotesis nula y tipos de error

35 / 48

Hipótesis nula y α

  • Entonces, el α es la probabilidad de error que fijamos para rechazar la hipótesis nula

  • en lenguaje de prueba de hipótesis, es la probabilidad de rechazar la hipótesis nula cuando esta es verdadera

  • o la probabilidad de encontrar diferencias entre grupos de la población cuando estas no existen

  • o en simple, la probabilidad de que nos estemos equivocando

36 / 48

Nivel de confianza y probabilidad de error α

  • el nivel de confianza de una estimación se determina de manera convencional, usualmente se acepta 95% o 99% de confianza

  • un nivel de confianza se expresa en una probabilidad de error α (alfa), que es 1- nivel de confianza

    • para un nivel de confianza de 95%, α=1−0.95=0.05

    • para un nivel de confianza de 99%, α=1−0.99=0.01

37 / 48

38 / 48

39 / 48

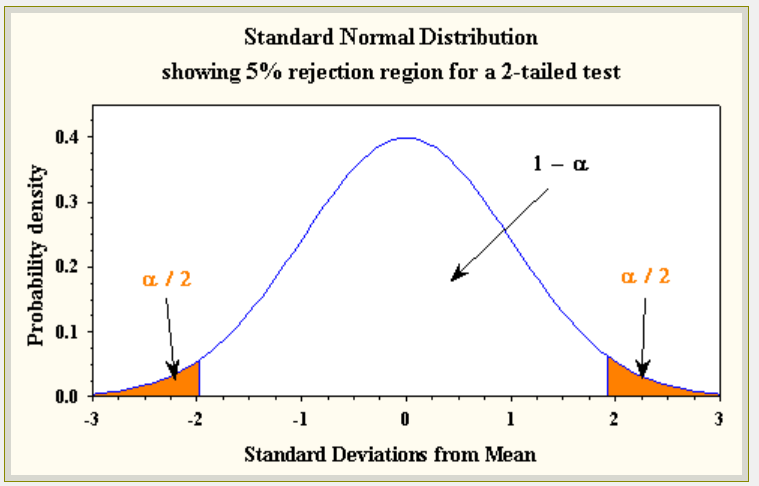
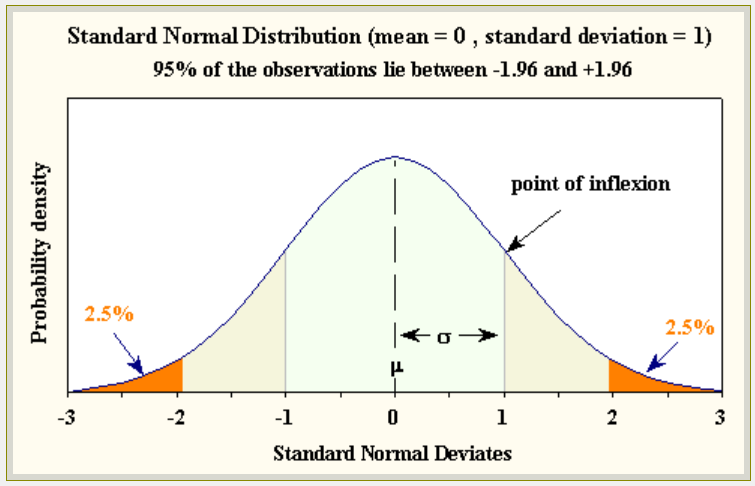
4. Intervalo de confianza [y contraste con valor crítico]

  • de la clase anterior con prueba Z sabemos que el valor crítico para un 95% de confianza es 1.96

  • para diferencia de medias se utiliza prueba t, donde el valor crítico es variable según en tamaño muestral

  • sin embargo, para muestras grandes, t=Z, y por lo tanto por ahora mantendremos los valores referenciales Z (de 1.96) hasta que profundicemos en t la próxima clase

40 / 48

4. Intervalo de confianza

ˉx1−ˉx2±tα/2∗SE¯x1−¯x250165±1.96∗5056150165±99099.56CI[−49287.48;149617.63]

41 / 48

Test de hipótesis de diferencias en R

t.test(salario ~ sexo, data = casen_350, var.equal=TRUE)
    Two Sample t-test
data:  salario by sexo
t = 0.99215, df = 341, p-value = 0.3218
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -49287.48 149617.63
sample estimates:
mean in group 1 mean in group 2 
       654585.4        604420.3
42 / 48

tabla t test con rempsyc

pacman::p_load(rempsyc,broom)
model <- t.test(salario ~ sexo, data = casen_350, var.equal=TRUE)
stats.table <- tidy(model, conf.int = TRUE)
nice_table(stats.table, broom = "t.test")
43 / 48

https://rempsyc.remi-theriault.com/articles/t-test

5. Interpretación

Nuestro intervalo de confianza contiene el cero, por lo que no se rechaza la hipótesis nula

Con un 95% de confianza (5% de probabilidad de error) no se encuentra evidencia de diferencias salariales entre hombres y mujeres.

Alternativamente: No existe evidencia que las diferencias salariales entre hombres y mujeres son distintas de cero, con un 5% de probabilidad de error

44 / 48

Resumen

  • hipótesis: aseveraciones sobre algo que ocurre en la población, usualmente asociaciones entre conceptos / variables

  • las hipótesis se contrastan con un criterio de falsabilidad

  • el contraste de hipótesis en estadística opera mediante el rechazo de la hipótesis nula (o de no diferencias), con una probabilidad de error α

  • 5 pasos para contraste de hipótesis

45 / 48

Próxima clase

  • Prueba t

  • hipótesis direccionales (mayor o menor qué) o de una cola (one tail)

  • inferencia para proporciones

46 / 48

Recomendaciones

47 / 48

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

48 / 48

¿Qué hemos visto hasta ahora?

... y ¿para qué?

2 / 48
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow