Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Sesión 6:

Inferencia 5: Prueba t y direccionalidad

1 / 52

2 / 52

Procedimiento: 5 pasos de la inferencia (ajustados de Ritchey)

Formular hipótesis ( $H_{0}$ y $H_{A}$ )
Obtener error estándar y estadístico de prueba empírico correspondiente (ej: Z o t)
Establecer la probabilidad de error $α$ (usualmente 0.05) y obtener valor crítico (teórico) de la prueba correspondiente
Cálculo de intervalo de confianza / contraste valores empírico/crítico
Interpretación

3 / 52

Pendientes:

prueba t
cálculo de valor crítico de prueba para contraste de hipótesis
hipótesis direccionales (por ejemplo, mayor o menor qué)

4 / 52

Prueba t5 / 52

Comparación entre grupos

gran parte de las hipótesis de investigación se relacionan con diferencias entre grupos, ej:
- hombres obtienen mayor salario que las mujeres
- los chilenos son más prejuiciosos que los migrantes
- ahora se apoyan los cambios más graduales que antes (comparación en el tiempo)

6 / 52

"la sociología comparada no es una rama especial de la sociología, sino que es la sociología misma en tanto deja de ser puramente descriptiva y aspira a dar razón de los hechos"

Durkheim (1895), Les règles de la méthode sociologique, op. cit., p. 137

7 / 52

Comparación de medias ( $\bar{X}$ )

en análisis cuantitativo, buena parte de las hipótesis comparativas remiten a comparaciones entre promedios o medias
- ej. (clase anterior): el promedio salarial de los hombres es mayor que el de las mujeres

8 / 52

Comparación de medias ( $\bar{X}$ )

en análisis cuantitativo, buena parte de las hipótesis comparativas remiten a comparaciones entre promedios o medias
- ej. (clase anterior): el promedio salarial de los hombres es mayor que el de las mujeres
la clase anterior realizamos una prueba Z para diferencia de medias solo a modo de simplificación, quedando pendiente el aplicar la prueba correspondiente: t

8 / 52

Del ejemplo de la clase anterior (sub muestra CASEN)

casen_350%>% # se especifica la base de datos
   dplyr::group_by(sexo=sjlabelled::as_label(sexo)) %>% # se agrupan por la variable categórica y se usan sus etiquetas con as_label
  dplyr::summarise(Obs.=n(),Promedio=mean(salario, na.rm=TRUE),SD=sd(salario, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla
  kable(, format = "markdown") # se genera la tabla

sexo	Obs.	Promedio	SD
1. Hombre	205	654585.4	468692.5
2. Mujer	138	604420.3	444666.0

Diferencia salarial = 654.585-604.420=50.165

9 / 52

Generación de intervalo (con Z)

$\begin{aligned} {\bar{x}}_{1} - {\bar{x}}_{2} & \pm t_{α / 2} * S E_{\bar{x_{1}} - \bar{x_{2}}} \\ 50165 & \pm 1.96 * 50561 \\ 50165 & \pm 99099.56 \\ C I [- 49287.48 & ; 149617.63] \end{aligned}$

Asumiendo que el valor crítico Z para un error $α$ de 0.5 (o 95% de confianza) es de 1.96

Para diferencia de medias necesitamos un valor crítico más preciso que el que nos da $Z$ , que se denomina el valor t .

10 / 52

$t$ y valores críticos

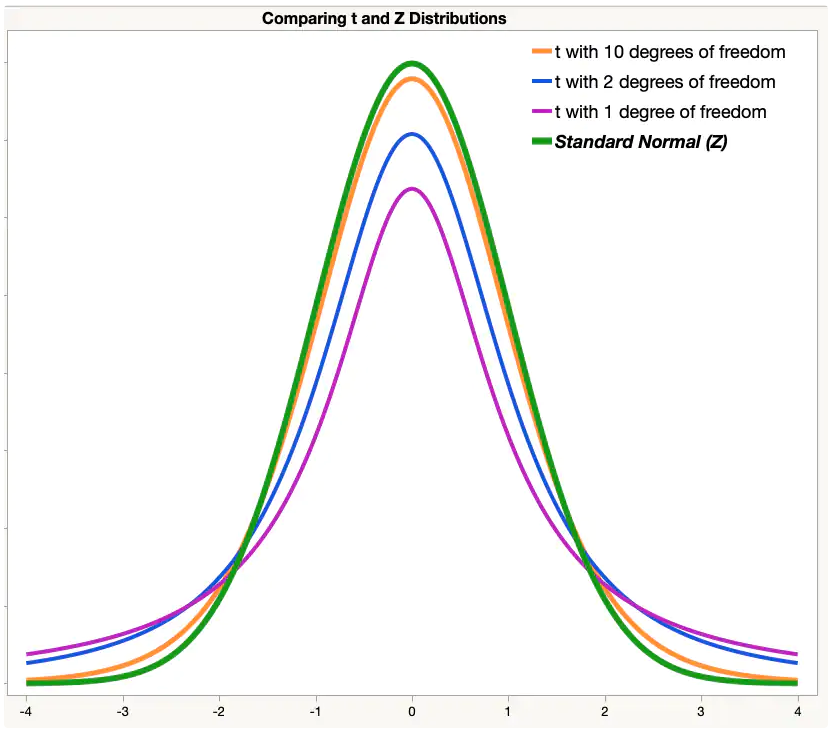
la distribución $t$ es similar a $Z$
se basa en la distribución normal, pero con ajuste para muestras pequeñas y para cuando no conocemos la desviación estándar de la población
por lo tanto, la forma de la distribución varía según el tamaño muestral, asociado al concepto de grados de libertad

11 / 52

12 / 52

Cálculo de valor crítico en Z

Recordemos el cáĺculo de valores críticos en Z para construir un intervalo de confianza al 95% (clase Inferencia 3):

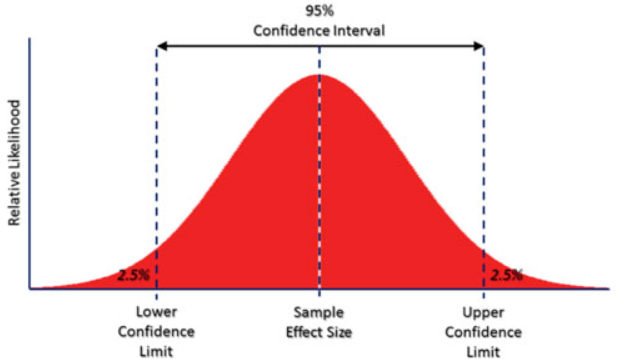
Límite inferior: 2.5% (0.025)

qnorm(0.025) # límite inferior

[1] -1.959964

Límite superior: 2.5% + 95% = 97.5% (0.975)

qnorm(0.975) # límite superior

[1] 1.959964

Y aproximando, $\pm$ 1.96

13 / 52

En el ejemplo de la clase anterior, para una diferencia de salarios de 50165, un error estándar de 50561, y un Z de 1.96=

$\begin{aligned} {\bar{x}}_{1} - {\bar{x}}_{2} & \pm [Z]_{α / 2} * S E_{\bar{x_{1}} - \bar{x_{2}}} \\ 50165 & \pm 1.96 * 50561 \\ 50165 & \pm 99099.56 \\ C I [- 49287.48 & ; 149617.63] \end{aligned}$

14 / 52

Intervalo de confianza para diferencia de medias con prueba $t$

la obtención del valor crítico para un determinado nivel de confianza es similar a Z, pero ajustado al tamaño muestral
el tamaño muestral se asocia al concepto de grados de libertad
la pregunta a responder es: ¿cuál es el valor crítico de $t$ para una probabilidad de error $α$ y grados de libertad $N - 2$ ?

15 / 52

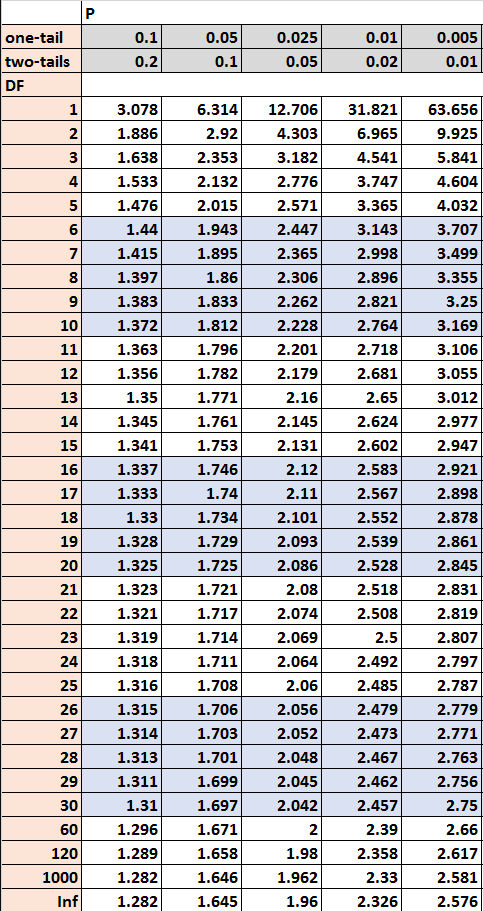
Para esto, tradicionalmente se recurre a la "tabla de valores $t$ "

A medida que aumenta la muestra (asociada a DF-grados de libertad), t se aproxima a Z

Como se ve en la tabla, en una muestra de 1000 el valor crítico para 0.025 t=1.96

16 / 52

Establecimiento del valor crítico de la prueba (t)

para un nivel de error $α = 0.05$
y una hipótesis de diferencia de dos colas: $α / 2 = [0.025 - 0.975]$
grados de libertad N-2= 343-2 = 341

qt(p=.05/2, df=341)

[1] -1.966945

qt(p=.05/2, df=341, 
   lower.tail=FALSE)

[1] 1.966945

Como vemos, es un poco mayor a Z pero parecido, ya que la muestra es de buen tamaño

17 / 52

Construcción de intervalo de confianza para diferencia de medias en base a prueba $t$

$\begin{aligned} {\bar{x}}_{1} - {\bar{x}}_{2} & \pm t_{α / 2} * S E_{\bar{x_{1}} - \bar{x_{2}}} \\ 50165 & \pm 1.967 * 50561 \\ 50165 & \pm 99453.49 \\ C I [- 49288.49 & ; 149618.5] \end{aligned}$

18 / 52

La prueba t de diferencia de medias considera el tamaño muestral (expresado en grados de libertad) para el cálculo del valor crítico
t se aproxima a Z a medida que aumenta el tamaño muestral
en muestras más pequeñas, t aumenta el nivel de exigencia al establecer valores críticos más altos que Z para poder rechazar la hipótesis nula

19 / 52

Prueba $t$ y test de hipótesis

además de la construcción de intervalos, otra forma más tradicional de test de hipótesis para diferencia de medias es la prueba $t$
la prueba $t$ consiste en el contraste de un valor crítico de $t$ con un valor empírico (o estadísitico) $t$ calculado con datos de nuestra muestra:

20 / 52

Prueba $t$ y test de hipótesis

además de la construcción de intervalos, otra forma más tradicional de test de hipótesis para diferencia de medias es la prueba $t$
la prueba $t$ consiste en el contraste de un valor crítico de $t$ con un valor empírico (o estadísitico) $t$ calculado con datos de nuestra muestra:

$t = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1} ²}{\sqrt{n_{1}}} + \frac{s_{2} ²}{\sqrt{n_{2}}}}}$

El denominador es el error estándar de la diferencia de promedios (que vimos la clase pasada)

20 / 52

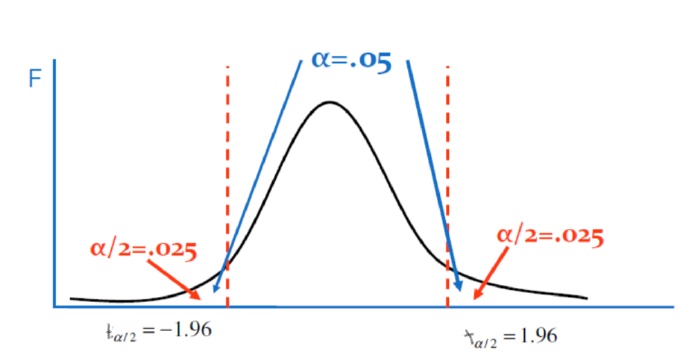
El valor $t$ calculado se compara con el valor crítico (teórico) de t asociado a una probabilidad de error $α$ , ej: 0.05

La prueba t es la comparación o contraste entre ambos valores. Si el t empírico es igual o superior al crítico se rechaza $H_{0}$

21 / 52

En nuestro ejemplo:

Para una diferencia de salarios de 50.165 y un error estándar de 50.561:

$t = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1} ²}{\sqrt{n_{1}}} + \frac{s_{2} ²}{\sqrt{n_{2}}}}} = \frac{50165}{50561} = 0.9921$

Este valor $t$ (empírico) se contrasta con el valor $t$ crítico correspondiente a un 5% de probabilidad de error

22 / 52

Prueba t

Contrastando ahora el valor calculado con el valor crítico:

$t_{c r t i t i c o} = - 1.96 < t_{c a l c u l a d o} = 0.992 < t_{c r i t i c o} = 1.96$

Por lo tanto, nuestro valor estimado queda fuera de la zona de rechazo de la hipótesis nula: la diferencia de medias no es estadísiticamente distinta de 0.
En consecuencia, con un nivel de confianza de 95% no podemos afirmar que existen diferencias salariales entre hombres y mujeres

23 / 52

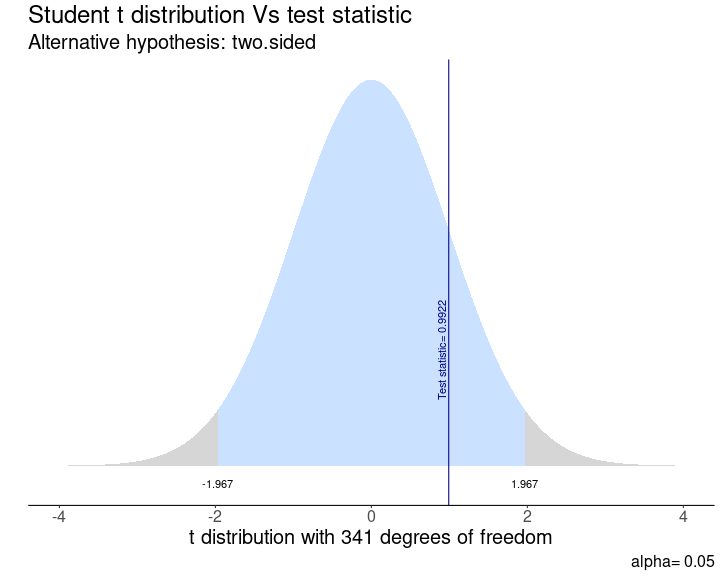
El gráfico muestra nuestro valor estimado de t fuera de la zona de rechazo (zona gris en la curva). Por lo tanto, no podemos rechazar $H_{0}$ , las diferencias no son distintas de cero

24 / 52

La prueba t consiste en un contraste entre el estadístico t (calculado a partir de nuestra muestra) y el valor crítico t para un nivel de error definido (usualmente 5%) 
25 / 52

La prueba t consiste en un contraste entre el estadístico t (calculado a partir de nuestra muestra) y el valor crítico t para un nivel de error definido (usualmente 5%)
Si el valor del estadísitico t no sobrepasa el valor crítico t, entonces no se logra rechazar la hipótesis nula, y no se puede afirmar que existen diferencias de medias en la población

25 / 52

La prueba t consiste en un contraste entre el estadístico t (calculado a partir de nuestra muestra) y el valor crítico t para un nivel de error definido (usualmente 5%)
Si el valor del estadísitico t no sobrepasa el valor crítico t, entonces no se logra rechazar la hipótesis nula, y no se puede afirmar que existen diferencias de medias en la población
Si el estadísitico t es superior al valor crítico, se rechaza la hipótesis nula

25 / 52

La prueba t consiste en un contraste entre el estadístico t (calculado a partir de nuestra muestra) y el valor crítico t para un nivel de error definido (usualmente 5%)
Si el valor del estadísitico t no sobrepasa el valor crítico t, entonces no se logra rechazar la hipótesis nula, y no se puede afirmar que existen diferencias de medias en la población
Si el estadísitico t es superior al valor crítico, se rechaza la hipótesis nula
La prueba t es la forma más tradicional de contrastar hipótesis de diferencia de medias, y se puede complementar con intervalos de confianza

25 / 52

$t$ y probabilidad de error $p$

el cálculo de $t$ (estimado) nos da un valor que puede ser transformado a un valor de área bajo la curva (tal como en Z)
cual es la probabilidad de error (valor p) de un $t$ específico?
hay que recordar que tanto Z como t tienen promedio 0 y son simétricas, y por lo tanto el 0 divide el área de la curva en 0.5
0.5 es la mayor probabilidad de error (=azar total), y a medida que se aleja del 0.5 disminuye la probabilidad de error

26 / 52

(qt(t,df, lower.tail = FALSE))*2

Donde:

qt: función que entrega la probabilidad para un valor $t$
df: grados de libertar (degrees of freedom)
lower.tail=FALSE: considera las probabilidades acumuladas hacia la cola superior de la curva
*2: al ser una prueba de diferencias, considera zona de rechazo en ambas direcciones de la curva, por lo que las probabilidades se multiplican por 2

27 / 52

En nuestro ejemplo:

(pt(0.99215, 341, lower.tail = FALSE))*2

[1] 0.3218278

La probabilidad de error del $t$ estimado es de 0.322.
Esto quiere decir es que en la estimación de esta diferencia de medias, nos estamos equivocando aproximadamente un tercio de las veces (lejos del nivel convencional de rechazo de $H_{0}$ de 0.05)

28 / 52

p y mayores niveles de confianza

La obtención del valor $p$ podría también entregar información para rechazar $H_{0}$ con un mayor nivel de confianza al establecido
Si bien el p<0.05 es aceptado, en el caso que el p sea menor a 0.01 o 0.001, se reporta por convención el valor p menor
Usualmente en los trabajos de investigación esto se representa con asteriscos: $^{*} p < 0.05$ , $^{* *} p < 0.01$ , y $^{* * *} p < 0.01$

29 / 52

A mayor valor tt, menor probabilidad de error pp30 / 52

Test de hipótesis: insumos complementarios

Entonces, se logra rechazar la hipótesis nula cuando:

el intervalo de confianza no contiene el 0
$t_{c a l c u l a d o} > t_{c r í t i c o}$
$p_{c a l c u l a d o} < p_{c r í t i c o}$

o en términos generales convencionales, p<0.05

31 / 52

Test de hipótesis de diferencias en R

t.test(salario ~ sexo, data = casen_350, var.equal=TRUE)


    Two Sample t-test
data:  salario by sexo
t = 0.99215, df = 341, p-value = 0.3218
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -49287.48 149617.63
sample estimates:
mean in group 1 mean in group 2 
       654585.4        604420.3

32 / 52

tabla t test con `rempsyc`

pacman::p_load(rempsyc,broom)
model <- t.test(salario ~ sexo, data = casen_350, var.equal=TRUE)
stats.table <- tidy(model, conf.int = TRUE)
nice_table(stats.table, broom = "t.test")

33 / 52

https://rempsyc.remi-theriault.com/articles/t-test

Reporte formato APA

"Se realizó una prueba t para muestras independientes para comparar los salarios entre hombres y mujeres. Los resultados indicaron una diferencia no significativa en los salarios entre hombres (M = 654585, SD = 468692) y mujeres (M = 604420, SD = 444666); t(341)=0.9921, p=0.321. El intervalo de confianza del 95% para la diferencia de medias fue [−49288.49;149618.5].

[diferencia no significativa=no se logra rechazar $H_{0}$ ]

34 / 52

En R con librería `report`

model <- t.test(salario ~ sexo, data = casen_350, var.equal=TRUE)
report(model)

La prueba t de dos muestras que evalúa la diferencia de salario según sexo (media en el grupo 1 = 654585, media en el grupo 2 = 604420) sugiere que el efecto es positivo, estadísticamente no significativo y muy pequeño (diferencia = 50165, IC del 95% [-49,287.48, 150,000], t(341) = 0.99, p = 0.322).

[traducido y con mínima edición]

35 / 52

Hipótesis direccionales36 / 52

Tipos de preguntas e hipótesis (ej: con promedio(s))

Pregunta	Hipotesis	Prueba
A. ¿Existe el promedio en la población?	$H_{a} : {\bar{X}}_{1} \neq 0$ $H_{0} : {\bar{X}}_{1} = 0$	Dos colas (no direccional)
B. ¿Existen diferencias de promedios en la población?	$H_{a} : {\bar{X}}_{1} - {\bar{X}}_{2} \neq 0$ $H_{0} : {\bar{X}}_{1} - {\bar{X}}_{2} = 0$	Dos colas (no direccional)
C. ¿Es un promedio (1) superior (o inferior) al otro (2)?	$H_{a} : {\bar{X}}_{1} - {\bar{X}}_{2} > 0$ $H_{0} : {\bar{X}}_{1} - {\bar{X}}_{2} \leq 0$	Una cola (direccional)

37 / 52

38 / 52

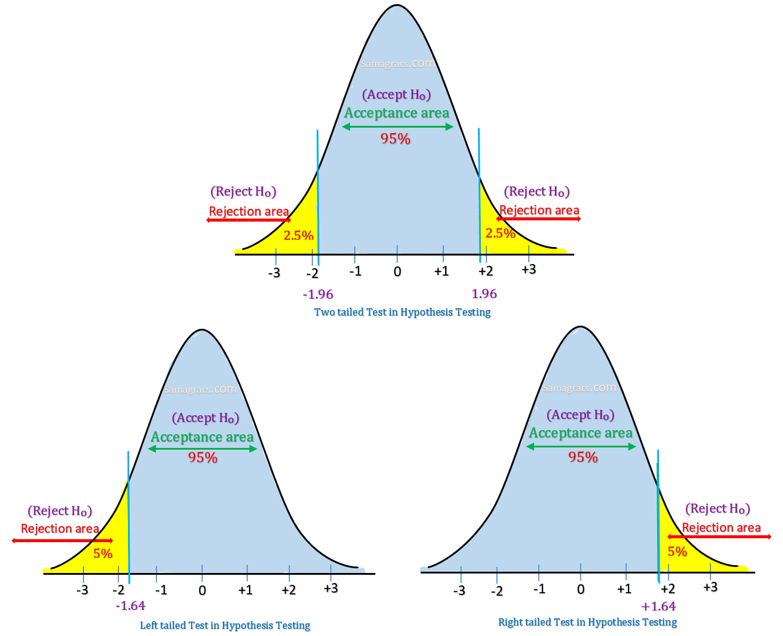
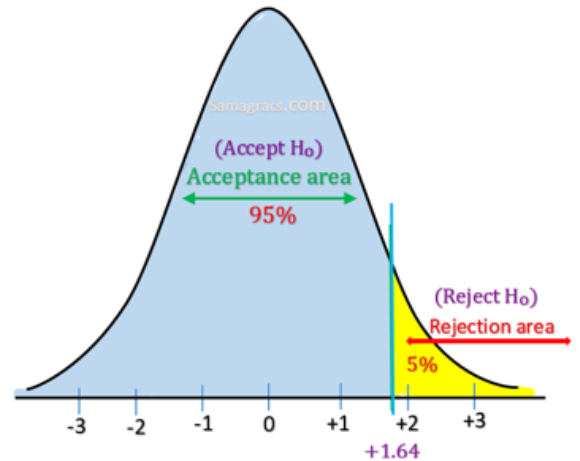
Si bien en teoría las hipótesis direccionales se pueden plantear en ambas direcciones, en general (y por simpleza) se expresan en términos de "mayor que", quedando la zona de rechazo de $H_{0}$ a la derecha

39 / 52

Pasos en test de hipótesis

Formulación: El salario de los hombres (grupo 1) es mayor al de las mujeres (grupo 2)

$\begin{aligned} H_{a} : {\bar{X}}_{1} > {\bar{X}}_{2} \\ H_{0} : {\bar{X}}_{1} \leq {\bar{X}}_{2} \end{aligned}$

2.Obtener error estándar y estadístico de prueba (lo mismo que para al caso anterior)

$t = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1} ²}{\sqrt{n_{1}}} + \frac{s_{2} ²}{\sqrt{n_{2}}}}} = \frac{50165}{50561} = 0.9921$

40 / 52

3.Probabilidad de error y valor crítico

seguimos con probabilidad de error ( $α$ 0.05), pero a diferencia de las no-direccionales no se divide entre 2 (colas), sino que es solo para una

41 / 52

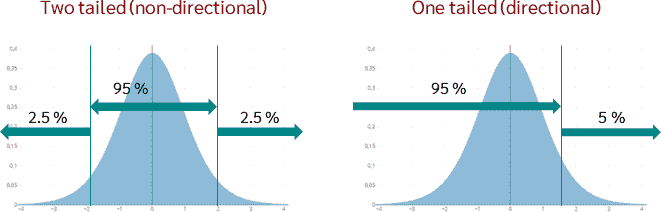
3.Probabilidad de error y valor crítico

para un nivel de error $α = 0.05$ (de una cola)
grados de libertad N-2= 343-2 = 341

qt(p=.05, 
   df=341,
   lower.tail = FALSE)

[1] 1.649334

[lower.tail=FALSE se refiere que el calculo refiere a la cola superior]

42 / 52

4.Contraste

Recordemos nuestra hipótesis nula:

$H_{0} : {\bar{X}}_{h o m b r e s} \leq {\bar{X}}_{m u j e r e s}$

Considerando los valores de contraste: $t_{e s t i m a d o} = 0.992 < t_{c r i t i c o} = 1.6$

43 / 52

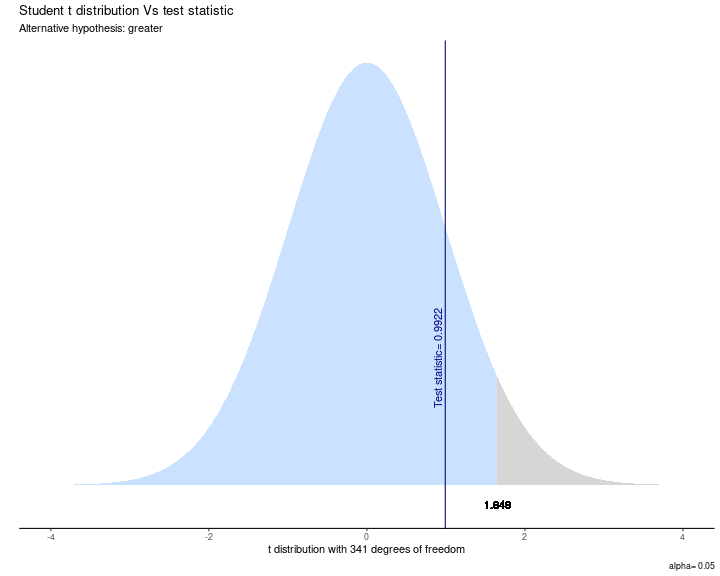
5. Interpretación

"Se realizó una prueba t para muestras independientes para examinar si el salario promedio de los hombres (M = 654585, SD = 468692) es mayor que el de las mujeres (M = 604420, SD = 444666), siendo la diferencia entre ambos de 50.165. Los resultados no fueron estadísticamente significativos, t(341)=0.9921, p=0.161. Por lo tanto, con un 95% de confianza no se puede rechazar la hipótesis nula, lo que no permite sustentar la hipótesis inicial (alternativa) que el salario de los hombres es mayor que el de las mujeres."

44 / 52

Nota: en el práctico cambiar el N de la muestra y establecer distintos niveles de confianza

¿Qué habría pasado con un tamaño muestral más grande, y/o con un nivel de probabilidad de error distinto?45 / 52

sub-muestra CASEN 1500 casos

casen_1500%>% # se especifica la base de datos
   dplyr::group_by(sexo=sjlabelled::as_label(sexo)) %>% # se agrupan por la variable categórica y se usan sus etiquetas con as_label
  dplyr::summarise(Obs.=n(),Promedio=mean(salario, na.rm=TRUE),SD=sd(salario, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla
  kable(, format = "markdown") # se genera la tabla

sexo	Obs.	Promedio	SD
1. Hombre	782	746620.7	828509.6
2. Mujer	662	605775.6	478087.6

46 / 52

model_dir2 <- t.test(
  salario ~ sexo, 
  data = casen_1500, 
  alternative="greater", 
  var.equal=TRUE, 
  conf.level = 0.95)
stats.table4 <- tidy(model_dir2)
nice_table(stats.table4, 
           broom = "t.test")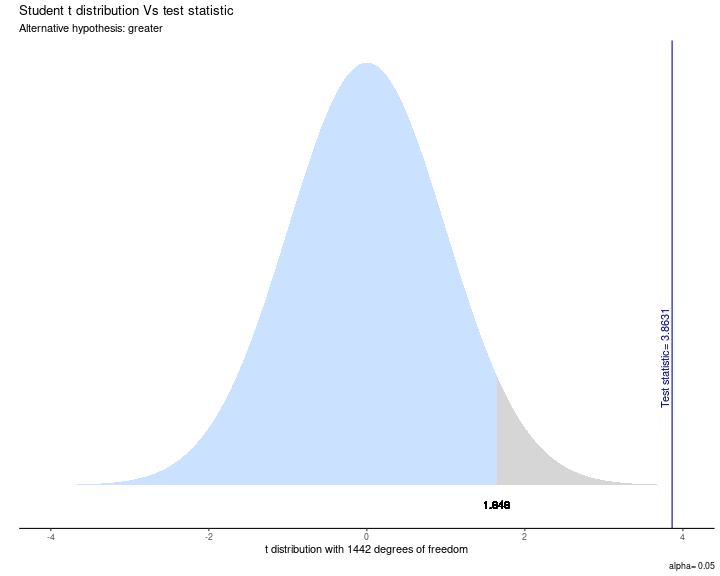

47 / 52

Resumen

t para diferencia de medias y ajuste por tamaño muestral / grados de libertad
prueba t por contraste entre valor del estadístico calculado (o t empírico) y el valor crítico para un nivel de confianza
valores p y reporte para valores convencionales menores a 0.05, 0.01o 0.001
hipótesis direccionales y no direccionales

48 / 52

Pendiente:hipótesis para proporciones, se verá en la próxima unidad en asociación entre variables categóricas
49 / 52

Recomendaciones:

Visualización interactiva de prueba t y valor p

50 / 52

51 / 52

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

52 / 52

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Sesión 6:

Inferencia 5: Prueba t y direccionalidad

Procedimiento: 5 pasos de la inferencia (ajustados de Ritchey)

Pendientes:

Prueba t

Comparación entre grupos

Comparación de medias ( ¯XX¯)

Comparación de medias ( ¯XX¯)

Del ejemplo de la clase anterior (sub muestra CASEN)

Generación de intervalo (con Z)

tt y valores críticos

Cálculo de valor crítico en Z

Intervalo de confianza para diferencia de medias con prueba tt

Establecimiento del valor crítico de la prueba (t)

Construcción de intervalo de confianza para diferencia de medias en base a prueba tt

Prueba tt y test de hipótesis

Prueba tt y test de hipótesis

t=(¯x1−¯x2)√s1²√n1+s2²√n2t=(x¯1−x¯2)s1²n1+s2²n2

En nuestro ejemplo:

t=(¯x1−¯x2)√s1²√n1+s2²√n2=5016550561=0.9921t=(x¯1−x¯2)s1²n1+s2²n2=5016550561=0.9921

Prueba t

tt y probabilidad de error pp

p y mayores niveles de confianza

A mayor valor tt, menor probabilidad de error pp

Test de hipótesis: insumos complementarios

tcalculado>tcríticotcalculado>tcrítico

pcalculado<pcríticopcalculado<pcrítico

Test de hipótesis de diferencias en R

tabla t test con rempsyc

Reporte formato APA

En R con librería report

Hipótesis direccionales

Tipos de preguntas e hipótesis (ej: con promedio(s))

Pasos en test de hipótesis

5. Interpretación

¿Qué habría pasado con un tamaño muestral más grande, y/o con un nivel de probabilidad de error distinto?

sub-muestra CASEN 1500 casos

Resumen

Pendiente:

Recomendaciones:

Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Help

Comparación de medias ( $\bar{X}$ )

Comparación de medias ( $\bar{X}$ )

$t$ y valores críticos

Intervalo de confianza para diferencia de medias con prueba $t$

Construcción de intervalo de confianza para diferencia de medias en base a prueba $t$

Prueba $t$ y test de hipótesis

Prueba $t$ y test de hipótesis

$t = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1} ²}{\sqrt{n_{1}}} + \frac{s_{2} ²}{\sqrt{n_{2}}}}}$

$t = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1} ²}{\sqrt{n_{1}}} + \frac{s_{2} ²}{\sqrt{n_{2}}}}} = \frac{50165}{50561} = 0.9921$

$t$ y probabilidad de error $p$

A mayor valor $t$ , menor probabilidad de error $p$

$t_{c a l c u l a d o} > t_{c r í t i c o}$

$p_{c a l c u l a d o} < p_{c r í t i c o}$

tabla t test con `rempsyc`

En R con librería `report`