Estadística Correlacional

Inferencia, asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.app

Sesión 10:

Correlación en ordinales, matrices e índices.

1 / 53

Correlación con variables ordinales2 / 53

Coeficiente de correlación de Spearman

se utiliza para variables ordinales y/o cuando se se violan supuestos de distribución normal
es equivalente a la correlación de Pearson del ranking de las observaciones analizadas
es alta cuando las observaciones tienen un ranking similar

3 / 53

Cálculo Spearman

se le asigna un número de ranking a cada valor
el valor más bajo obtiene el mayor ranking, y el más alto el menor
en caso de valores repetidos se produce un "empate", y entonces el ranking se promedia.

4 / 53

Ejemplo: variable Educación

data$educ

[1] 2 3 4 4 5 7 8 8

Como estos valores están ordenados de menor a mayor, entonces en principio los valores de ranking serían:

8 7 6 5 4 3 2 1.

Pero, hay un par de empates

el valor 4 está repetido y corresponden a los ranking 6 y 5, por lo tanto a ambos se les asigna el promedio de estos rankings: 5,5
lo mismo sucede con el valor 8 en los rankings 2 y 1, por lo tanto a ambos se les asigna el valor 1,5

5 / 53

data

  id educ ing mean_educ dif_m_educ dif_m_educ2 mean_ing dif_m_ing
1    2   1     5.125     -3.125    9.765625    5.375    -4.375
2    3   3     5.125     -2.125    4.515625    5.375    -2.375
3    4   3     5.125     -1.125    1.265625    5.375    -2.375
4    4   5     5.125     -1.125    1.265625    5.375    -0.375
5    5   4     5.125     -0.125    0.015625    5.375    -1.375
6    7   7     5.125      1.875    3.515625    5.375     1.625
7    8   9     5.125      2.875    8.265625    5.375     3.625
8    8  11     5.125      2.875    8.265625    5.375     5.625
  dif_m_ing2    dif_xy predict
19.140625 13.671875     1.0
 5.640625  5.046875     2.4
 5.640625  2.671875     3.8
 0.140625  0.421875     3.8
 1.890625  0.171875     5.2
 2.640625  3.046875     8.0
13.140625 10.421875     9.4
31.640625 16.171875     9.4
/ 53

data %>%
  select (educ, ing)

  educ ing
  2   1
  3   3
  4   3
  4   5
  5   4
  7   7
  8   9
  8  11
/ 53

data %>%
  select (educ, ing) %>%
  mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5))

  educ ing educ_rank
1    2   1       8.0
2    3   3       7.0
3    4   3       5.5
4    4   5       5.5
5    5   4       4.0
6    7   7       3.0
7    8   9       1.5
8    8  11       1.5
5 / 53

data %>%
  select (educ, ing) %>%
  mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5)) %>%
  mutate(., ing_rank=c(8,6.5,6.5,4,5,3,2,1))

  educ ing educ_rank ing_rank
1    2   1       8.0      8.0
2    3   3       7.0      6.5
3    4   3       5.5      6.5
4    4   5       5.5      4.0
5    5   4       4.0      5.0
6    7   7       3.0      3.0
7    8   9       1.5      2.0
8    8  11       1.5      1.0
5 / 53

data %>%
  select (educ, ing) %>%
  mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5)) %>%
  mutate(., ing_rank=c(8,6.5,6.5,4,5,3,2,1))
cor(data_spr$educ_rank, data_spr$ing_rank)

  educ ing educ_rank ing_rank
1    2   1       8.0      8.0
2    3   3       7.0      6.5
3    4   3       5.5      6.5
4    4   5       5.5      4.0
5    5   4       4.0      5.0
6    7   7       3.0      3.0
7    8   9       1.5      2.0
8    8  11       1.5      1.0
[1] 0.9394112
5 / 53

Cálculo directo en R:

cor.test(data$educ, data$ing, "two.sided", "spearman")


    Spearman's rank correlation rho
data:  data$educ and data$ing
S = 5.0895, p-value = 0.0005311
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.9394112

6 / 53

El coeficiente de correlación de Spearman no es más que una correlación de Pearson del ranking de las variables7 / 53

Coeficiente de correlación Tau de Kendall

Recomendado cuando hay un set de datos pequeños y/o cuando hay mucha repetición de observaciones en el mismo ranking
Se basa en una comparación de pares de observaciones concordantes y discordantes

8 / 53

Coeficiente de correlación Tau de Kendall

Recomendado cuando hay un set de datos pequeños y/o cuando hay mucha repetición de observaciones en el mismo ranking
Se basa en una comparación de pares de observaciones concordantes y discordantes

En R:

cor.test(data$educ, data$ing,
         "two.sided", 
         "kendall")


    Kendall's rank correlation tau
data:  data$educ and data$ing
z = 2.9115, p-value = 0.003597
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.8680791

8 / 53

Recomendaciones generales

Pearson es el coeficiente de correlación por defecto
En caso de datos en escala de medición ordinal se puede aplicar Spearman (aunque Pearson es también aceptado en este contexto).
Kendall se reporta en casos muy específicos donde hay un set de datos pequeños y repetición de observaciones en el mismo ranking ("empates")

9 / 53

Matrices de correlación10 / 53

Matriz de correlaciónuna matriz de correlación se conforma cuando se representa simultaneamente más de un par de asociaciones bivariadas
11 / 53

Matriz de correlación

una matriz de correlación se conforma cuando se representa simultaneamente más de un par de asociaciones bivariadas

por ejemplo, si agregamos la variable edad a nuestra base de datos:

data$edad <- c(50, 65, 27, 15, 40, 22, 25, 38)

Tenemos 3 variables, y por lo tanto los siguentes pares de correlaciones posibles: ingreso-educación, ingreso-edad, y educación-edad

11 / 53

cor_mat <- data

11 / 53

cor_mat <- data %>%
  select(educ, ing, edad)

11 / 53

cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)

11 / 53

cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
cor_mat

           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
11 / 53

cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
cor_mat
round(cor_mat, 3)

           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
       educ    ing   edad
educ  1.000  0.951 -0.470
ing   0.951  1.000 -0.406
edad -0.470 -0.406  1.000
11 / 53

cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
cor_mat
round(cor_mat, 3)
sjPlot::tab_corr(cor_mat)

           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
       educ    ing   edad
educ  1.000  0.951 -0.470
ing   0.951  1.000 -0.406
edad -0.470 -0.406  1.000


 
educ
ing
edad

educ
 
0.951
-0.470

ing
0.951
 
-0.406

edad
-0.470
-0.406
 

Computed correlation used pearson-method with listwise-deletion.

11 / 53

	educ	ing	edad
educ		0.951	-0.470
ing	0.951		-0.406
edad	-0.470	-0.406
Computed correlation used pearson-method with listwise-deletion.

Matriz de correlación(es)tabla de doble entrada donde las variables se presentan tanto en las filas como en las columnas
12 / 53

Matriz de correlación(es)

tabla de doble entrada donde las variables se presentan tanto en las filas como en las columnas
el coeficiente de correlación correspondiente al par de variables aparece en la intersección de las columnas

12 / 53

Matriz de correlación(es)

tabla de doble entrada donde las variables se presentan tanto en las filas como en las columnas
el coeficiente de correlación correspondiente al par de variables aparece en la intersección de las columnas
existe información redundante
- las correlaciones se repiten, dado que las variables se intersectan dos veces en la tabla
- la diagonal tiene solo unos (1), ya que es la correlación de la variable consigo misma

12 / 53

Ajustando tabla sjPlot::tab_corr

sjPlot::tab_corr(cor_mat,
  triangle = "lower",
  title = "Tabla de correlaciones del ejemplo"
  )

Tabla de correlaciones del ejemplo
	educ	ing
educ
ing	0.951
edad	-0.470	-0.406
Computed correlation used pearson-method with listwise-deletion.

12 / 53

Matriz con librería  corrplotlibrary(corrplot)

12 / 53

Matriz con librería corrplot

library(corrplot)
corrplot(cor_mat)

12 / 53

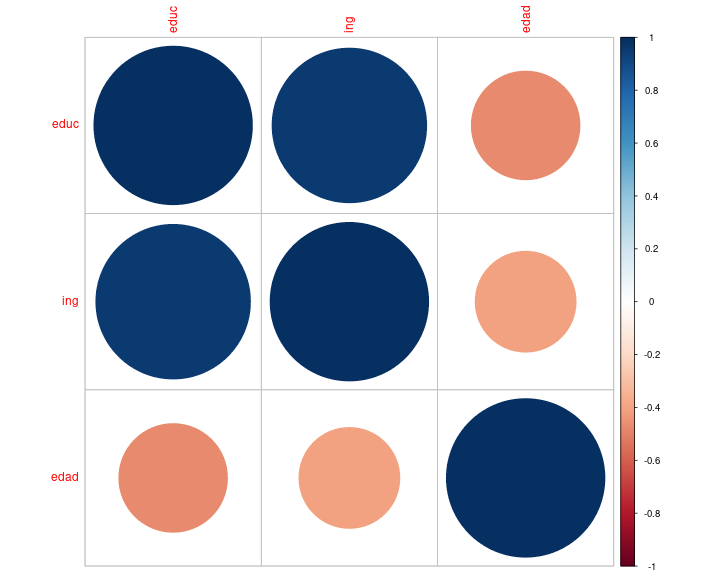
Matriz con librería corrplot

corrplot(cor_mat,
  method = 'number')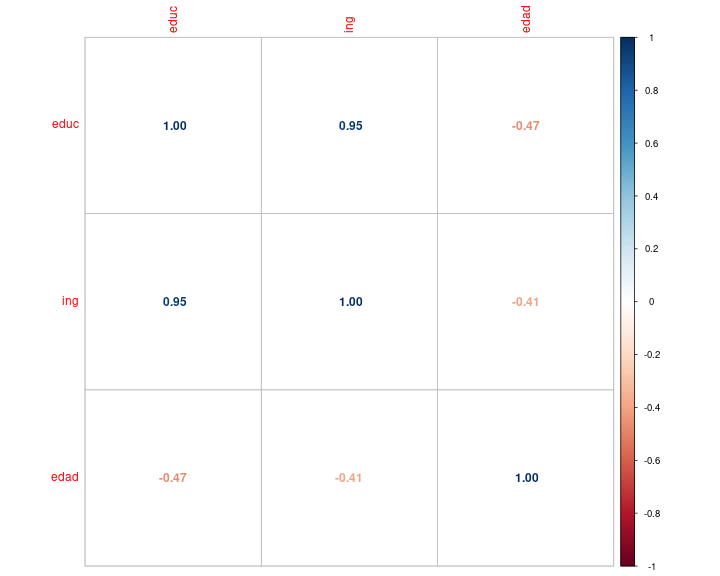

12 / 53

corrplot

corrplot(cor_mat,
  method = 'number',
  type = 'lower',
  number.cex = 3,
  tl.cex = 3,
  diag = FALSE)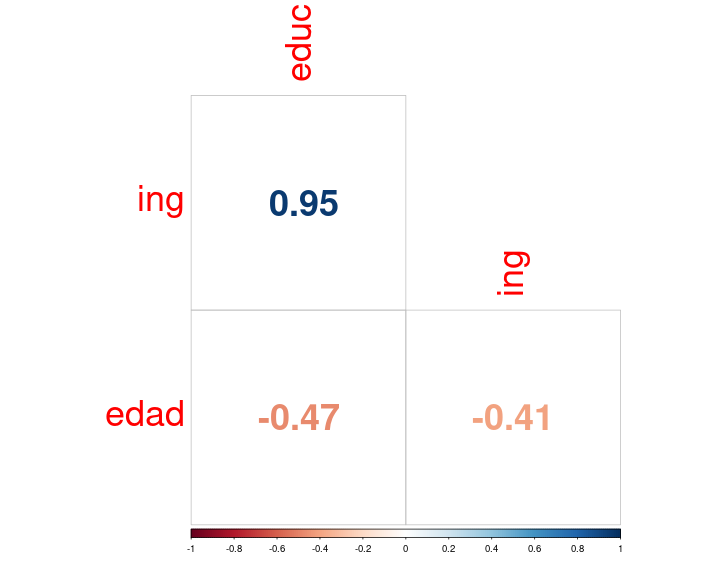

12 / 53

corrplot.mixed

corrplot.mixed(cor_mat,
  lower = "number",
  upper = "circle",
  number.cex = 3,
  tl.cex = 3,
  diag = "n")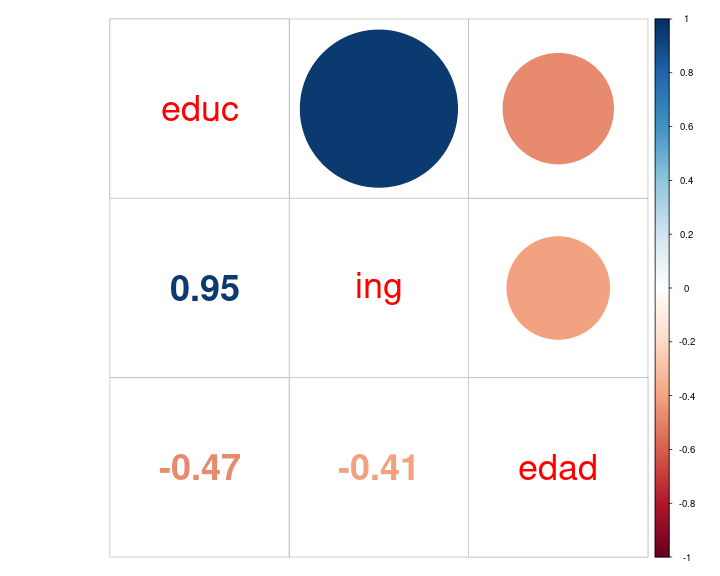

12 / 53

corrplot.mixed

corrplot(cor_mat,
  type = "lower",
  addCoef.col = 'white',
  number.cex = 3,
  tl.cex = 3,
  diag = FALSE)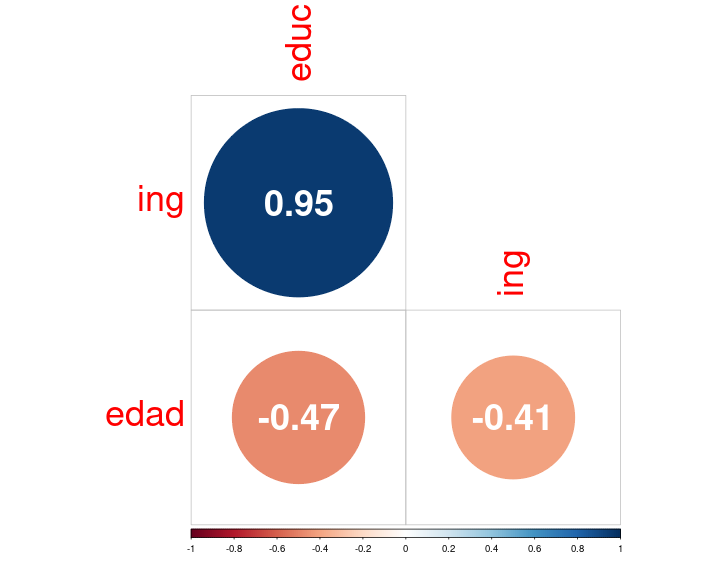

12 / 53

corrplot.mixed

corrplot(cor_mat,
  type = "lower",
  addCoef.col = 'white',
  number.cex = 3,
  tl.cex = 3,
  diag = FALSE,
  method = 'square')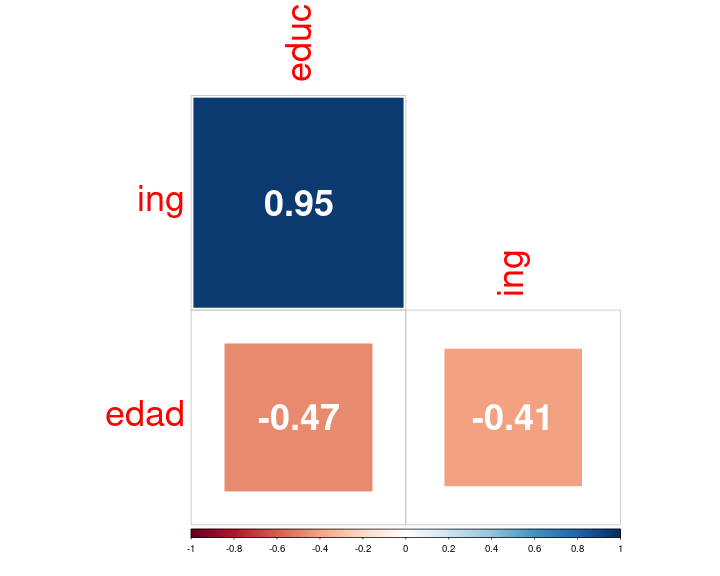

12 / 53

Correlaciones, matrices, y casos perdidos13 / 53

Consideraciones sobre casos perdidos

Cuando hay casos perdidos en las variables, ¿cuál es el número de casos de la matriz de correlaciones?
Las correlaciones bivariadas se calculan con información completa, por lo tanto si hay un dato perdido en una de las variables se elimina el caso completo
Algunas funciones lo hacen de manera automática, en otras hay que especificarlo previamente

14 / 53

Ejemplo

Agreguemos un caso perdido (NA en R) a una de nuestras variables

data$edad

[1] 50 65 27 15 40 22 25 38

data$edad <-replace(data$edad, data$edad==15, NA)
data$edad

[1] 50 65 27 NA 40 22 25 38

15 / 53

cormat_NA <- data %>% select(educ, ing, edad) %>% cor(.)
round(cormat_NA,3)

      educ   ing edad
educ 1.000 0.951   NA
ing  0.951 1.000   NA
edad    NA    NA    1
cormat_listwise <- data %>% select(educ, ing, edad) %>% 
  cor(., use = "complete.obs")
round(cormat_listwise, 3)

       educ    ing   edad
educ  1.000  0.962 -0.669
ing   0.962  1.000 -0.494
edad -0.669 -0.494  1.000
16 / 53

Eliminación de casos perdidos por lista (o listwise)

las correlaciones bivariadas requieren eliminación de casos perdidos tipo listwise, es decir, si hay un dato perdido en una variable se pierde el caso completo
Para conocer el número de casos con que se calculó la matriz:

sum(complete.cases(data))

[1] 7

Por lo tanto, en el cálculo se perdió el caso o fila completa de la base (de 8 casos) que tenía el caso perdido.

17 / 53

Eliminación de casos perdidos por pares (o pairwise)

en el caso de las matrices de correlaciones es posible tomar la opción pairwise para casos perdidos
pairwise quiere decir que se eliminan los casos perdidos solo cuando afectan al cálculo de un par específico.

18 / 53

Eliminación de casos perdidos por pares (o pairwise)

en el caso de nuestro ejemplo, si consideramos listwise todas las correlaciones tienen 7 casos, pero con pairwise la correlación entre educación e ingreso mantendría 8 casos.
por lo tanto, pairwise permite mayor rescate de información y mayor N en el cálculo de matrices de correlaciones

19 / 53

Opción pairwise en correlación en R

data %>% select(educ, ing, edad) %>% 
  cor(., use = "pairwise")

           educ        ing       edad
educ  1.0000000  0.9512367 -0.6693607
ing   0.9512367  1.0000000 -0.4941732
edad -0.6693607 -0.4941732  1.0000000

En este caso vemos una leve variación en el coeficiente comprometido (educ-ing) comparando listwise con pairwise

20 / 53

Número de casos pairwise

data %>% select(educ,ing,edad) %>% psych::pairwiseCount()

     educ ing edad
educ    8   8    7
ing     8   8    7
edad    7   7    7

Se indica que en las correlaciones con edad se utilizaron 7 casos, mientras en la correlación entre ingreso y educación se utilizan 8 casos con el método pairwise

21 / 53

Baterías, matrices y consistencia22 / 53

23 / 53

Preguntas y error de medición

Para medir hechos observables simples usualmente se utiliza una pregunta (ej: edad)
Fenómenos complejos se miden en general con más de una pregunta, con el objetivo de dar mejor cuenta del atributo (i.e. minimizar error de medición)

24 / 53

Baterías de indicadores múltiplesen general las encuestas suelen incluir varias preguntas respecto de un mismo tema -> baterías de indicadores múltiples
25 / 53

Baterías de indicadores múltiples

en general las encuestas suelen incluir varias preguntas respecto de un mismo tema -> baterías de indicadores múltiples
cubren distintos aspectos de un mismo fenómeno complejo que no se agota en solo un indicador -> minimiza error de medición

25 / 53

Baterías de indicadores múltiples

en general las encuestas suelen incluir varias preguntas respecto de un mismo tema -> baterías de indicadores múltiples
cubren distintos aspectos de un mismo fenómeno complejo que no se agota en solo un indicador -> minimiza error de medición
problema: ¿cómo se analizan indicadores que están relacionados?¿cómo se muestran los resultados?

25 / 53

Análisis de indicadores en baterías

Univariado: se sugiere presentar análisis descriptivos que contengan todos los indicadores para poder comparar frecuencias

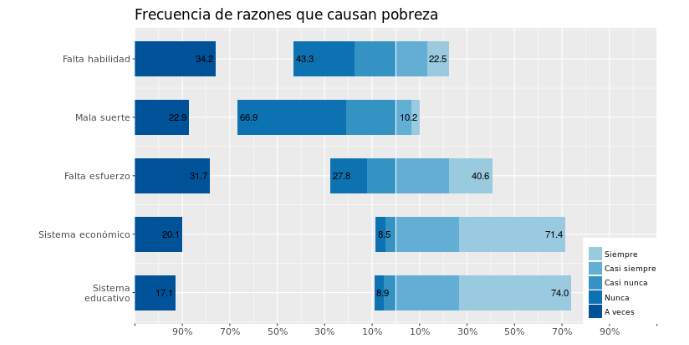(likert plot, sjPlot)

26 / 53

Análisis de indicadores en baterías

2. Bivariado: tablas/gráficos de correlaciones

(corrplot)

27 / 53

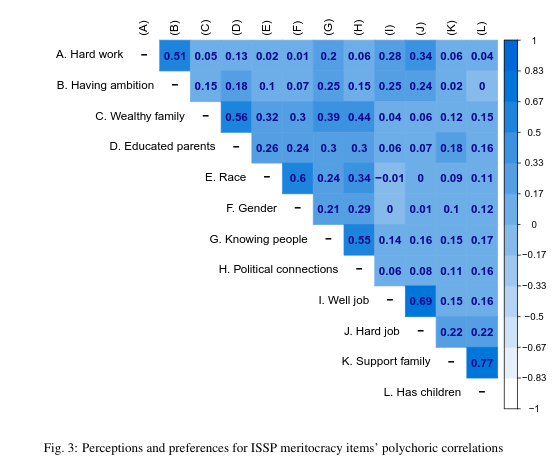
Análisis de indicadores en baterías

Se podría asumir un concepto o dimensión subyacente a la batería de items
Para facilitar el avance en el análisis (por ejemplo, relacionar ese concepto subyacente con otras variables), muchas veces se reduce la batería a algún tipo de índice (sumativo/promedio)
¿Podemos asegurar que los items están realmente midiendo lo mismo?

28 / 53

¿Miden lo mismo?

29 / 53

Preguntas y error de medición

En este marco se asume que el indicador es distinto del atributo, y que la medición del atributo o variable latente conlleva error
Cuando la el atributo se mide con más de una pregunta, se puede intentar estimar la variable latente mediante índices o técnicas de análisis factorial

30 / 53

Medición y error

antes de agrupar indicadores en un índice hay que evaluar si los indicadores se encuentran relacionados
- -> si miden constructos similares
- -> si la medición es confiable

31 / 53

¿Cómo estimar el nivel de relación entre indicadores que miden un mismo constructo?

32 / 53

¿Cómo estimar el nivel de relación entre indicadores que miden un mismo constructo?

Distintas maneras, pero todas se basan en la técnica de la correlación

32 / 53

Matriz de correlaciones (1)

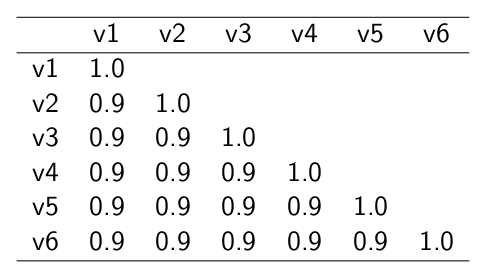
Matriz hipotética de indicadores que miden un mismo constructo

33 / 53

Ej. Matriz de correlaciones (2)

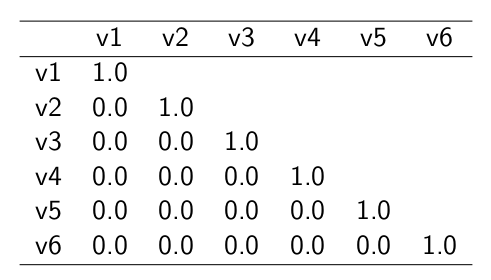
Matriz hipotética de indicadores que miden constructos independientes

34 / 53

Ej. Matriz de correlaciones (3)

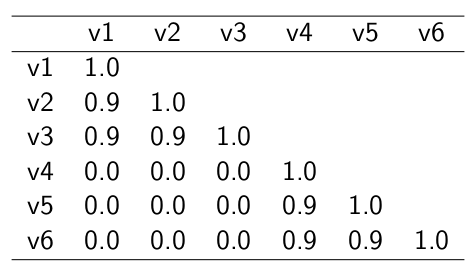
Matriz hipotética de variables que miden dos constructos independientes

35 / 53

Entonces:1. analizar la matriz de correlaciones antes de generar cualquier técnica de reducción de información (ej: crear índice)2. evaluar la posibilidad de generación algún tipo de índice que resuma la información36 / 53

Datos ejemplo

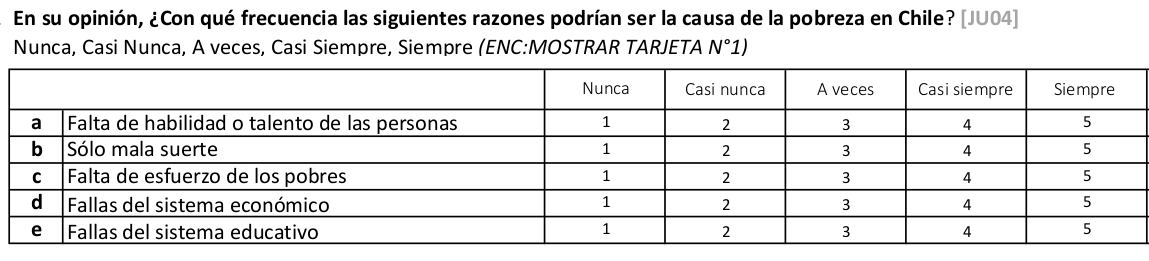
batería atribuciones de pobreza, encuesta "Desigualdad, Justicia y Participación Política" - FONDECYT Iniciación 11121203 (2013-2015) Social justice and citizenship participation

37 / 53

var
label
n
NA.prc
mean
sd
range


2
falthab
Razones pobreza falta de habilidad
1228
1.365462
2.630293
1.254220
4 (1-5)

3
malasue
Razones pobreza mala suerte
1227
1.445783
2.019560
1.140079
4 (1-5)

1
faltesf
Razones pobreza falta de esfuerzo
1238
0.562249
3.155897
1.290758
4 (1-5)

4
sisecon
Razones pobreza sistema económico
1218
2.168675
4.036946
1.095047
4 (1-5)

5
siseduc
Razones pobreza sistema educativo
1227
1.445783
4.088835
1.088767
4 (1-5)


38 / 53

	var	label	n	NA.prc	mean	sd	range
2	falthab	Razones pobreza falta de habilidad	1228	1.365462	2.630293	1.254220	4 (1-5)
3	malasue	Razones pobreza mala suerte	1227	1.445783	2.019560	1.140079	4 (1-5)
1	faltesf	Razones pobreza falta de esfuerzo	1238	0.562249	3.155897	1.290758	4 (1-5)
4	sisecon	Razones pobreza sistema económico	1218	2.168675	4.036946	1.095047	4 (1-5)
5	siseduc	Razones pobreza sistema educativo	1227	1.445783	4.088835	1.088767	4 (1-5)

Matriz de correlaciones

cormat <- cor(data)
cormat

        falthab malasue faltesf sisecon siseduc
falthab       1      NA      NA      NA      NA
malasue      NA       1      NA      NA      NA
faltesf      NA      NA       1      NA      NA
sisecon      NA      NA      NA       1      NA
siseduc      NA      NA      NA      NA       1

Esta función no resulta ya que requiere que no existan casos perdidos

39 / 53

Matriz de correlaciones

Entonces:

cormat <- cor(na.omit(data))
cormat

             falthab    malasue     faltesf     sisecon      siseduc
falthab  1.000000000 0.31793357  0.36246039 -0.02787884 -0.005893529
malasue  0.317933565 1.00000000  0.16936872  0.02755708  0.013865045
faltesf  0.362460395 0.16936872  1.00000000 -0.06579454 -0.020114542
sisecon -0.027878843 0.02755708 -0.06579454  1.00000000  0.593625639
siseduc -0.005893529 0.01386504 -0.02011454  0.59362564  1.000000000

40 / 53

Matriz de correlaciones (Formato publicable)tab_corr(data)



 
Razones pobreza falta de habilidad
Razones pobreza mala suerte
Razones pobreza falta de esfuerzo
Razones pobreza sistema económico
Razones pobreza sistema educativo

Razones pobreza falta de habilidad
 
0.318***
0.362***
-0.028
-0.006

Razones pobreza mala suerte
0.318***
 
0.169***
0.028
0.014

Razones pobreza falta de esfuerzo
0.362***
0.169***
 
-0.066*
-0.020

Razones pobreza sistema económico
-0.028
0.028
-0.066*
 
0.594***

Razones pobreza sistema educativo
-0.006
0.014
-0.020
0.594***
 

Computed correlation used pearson-method with listwise-deletion.

41 / 53

	Razones pobreza falta de habilidad	Razones pobreza mala suerte	Razones pobreza falta de esfuerzo	Razones pobreza sistema económico	Razones pobreza sistema educativo
Razones pobreza falta de habilidad		0.318***	0.362***	-0.028	-0.006
Razones pobreza mala suerte	0.318***		0.169***	0.028	0.014
Razones pobreza falta de esfuerzo	0.362***	0.169***		-0.066*	-0.020
Razones pobreza sistema económico	-0.028	0.028	-0.066*		0.594***
Razones pobreza sistema educativo	-0.006	0.014	-0.020	0.594***
Computed correlation used pearson-method with listwise-deletion.

Matriz de correlaciones - gráfico

corrplot(cormat)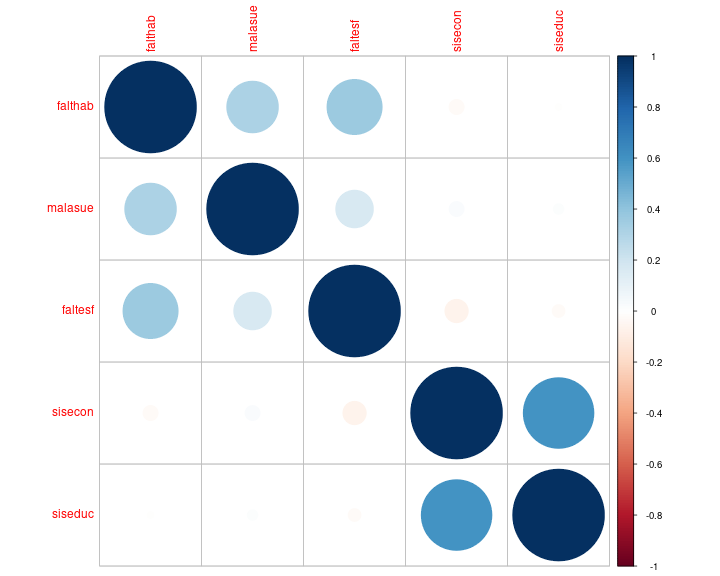

42 / 53

Matriz de correlaciones - gráfico ajustado

  corrplot::corrplot(cormat,
    method = "color",
    addCoef.col = "#000390",
    type = "upper",
    tl.col = "black",
    col=colorRampPalette(c("white","#0068DC"))(8),
    bg = "white",
    na.label = "-")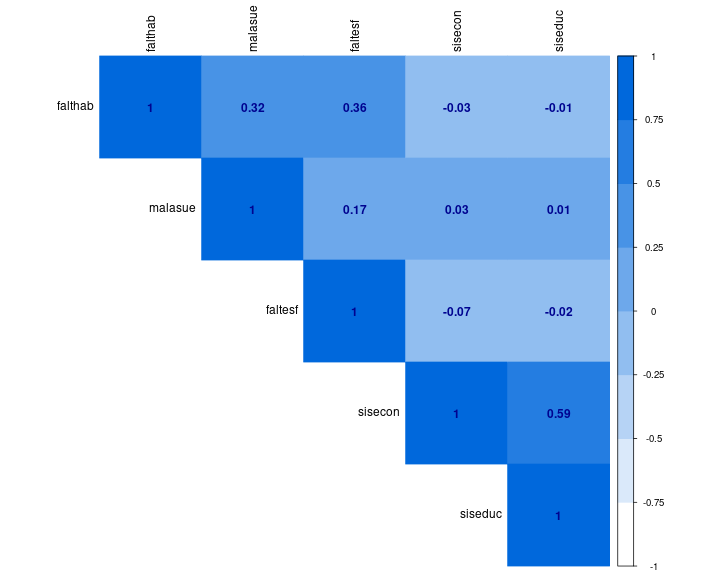

43 / 53

Hacia la construcción de un índice44 / 53

Alpha de Cronbach

índice de consistencia interna de una batería
en general, interpretable como la correlación [absoluta] promedio entre distintas variables que componen una batería de medición
varía entre 0 y 1; valores más cercanos a 1 indican mayor consistencia
en general valores sobre 0.6 se consideran aceptables

45 / 53

Alpha de Cronbach

funcion alpha de la librería psych
se genera un objeto (lo llamaremos alpha). Contiene bastante información, por ahora nos enfocaremos solo en el valor de alpha (raw_alpha)

names(data)

[1] "falthab" "malasue" "faltesf" "sisecon" "siseduc"

alpha <-psych::alpha(data)

Some items ( falthab malasue faltesf ) were negatively correlated with the total scale and 
probably should be reversed.  
To do this, run the function again with the 'check.keys=TRUE' option

alpha$total$raw_alpha

[1] 0.4363206

46 / 53

Alpha de Cronbach

puntaje 0.43, por lo tanto bajo los valores aceptables de consistencia interna
esto ya se podía anticipar desde la matriz de correlaciones, que aparentemente mostraba dos dimensiones subyacentes a la batería
además, se genera un mensaje de advertencia sobre posibles items codificados a la inversa (dada la correlación entre items de dimensiones distintas)

47 / 53

Opciones

construcción de índices basados en la información de la matriz de correlaciones
análisis factorial

48 / 53

Construcción de índices49 / 53

Índice promedio

vamos a generar 2 índices a partir de esta batería: uno para atribución interna (falthab,faltesf,malasue) y otro para externa (sisecon,siseduc)
tema valores perdidos:
- para perder el mínimo de casos se recomienda realizar índice aún con casos que no hayan respondido algún item
- ya que esto distorsionaría el puntaje si fuera sumado, se hace un índice promedio, especificando que se calcule aún con valores perdidos

50 / 53

Indice de atribución interna y externa (promedios)

data <- cbind(data, "interna_prom"=rowMeans(data %>% select(falthab,faltesf,malasue), na.rm=TRUE))
data <- cbind(data, "externa_prom"=rowMeans(data %>% select(sisecon,siseduc), na.rm=TRUE))
names(data)

[1] "falthab"      "malasue"      "faltesf"      "sisecon"     
[5] "siseduc"      "interna_prom" "externa_prom"

51 / 53

Resumen- Correlación de Spearman: apropiada para variables ordinales, equivale a la correlación de Pearson del ranking de las variables
- Matriz de correlaciones: forma tradicional de reporte de asociaciones de las variables de una investigación, importante considerar tratamiento de datos perdidos (listwise o pairwise)
- Índices y consistencia interna en matrices52 / 53

Estadística Correlacional

Inferencia, Asociación y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2024

correlacional.netlify.com

53 / 53

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help