Estadística Correlacional

class: front

.pull-left-wide[
# Estadística Correlacional]

.pull-right-narrow[![:scale 85%](img/logo-correlacional-transp.png)]

## Inferencia, asociación y reporte

----
.pull-left[

## Juan Carlos Castillo
## Sociología FACSO - UChile
## 2do Sem 2024
## [.orange[correlacional.netlify.app]](https:/correlacional.netlify.app)
]

.pull-right-narrow[
.center[
.content-block-gray[
## .gray[Sesión 12:] 
## .curso[Asociación con variables categóricas 2]]
]
]
---

layout: true
class: animated, fadeIn

---
# Tipos de correlación según nivel de medición
----

.small[

|                       | **Nominal Dicotómica**      | **Nominal Politómica**      | **Ordinal**                 | **Intervalar/Razón**       |
|-----------------------|----------------------------|----------------------------|----------------------------|---------------------------|
| **Nominal Dicotómica**|       Tetracórica      |                 |                     Biserial        | Punto Biserial  |
| **Nominal Politómica**|                |                 |                             |                            |
| **Ordinal**           |     Biserial                       |                            | Spearman, Kendall           | Pearson/biserial, Policórica                |
| **Intervalar/Razón**  | Punto Biserial   |                            | Pearson/biserial, Policórica                 | Pearson                   |

]

---
class: inverse bottom right

# Asociación en tablas de contingencia

---
## Escalas de medición de variables

- NOIR: Nominal, Ordinal, Intervalar, Razón

.small[
| Tipo       	| Características                     	        | Propiedad de números 	| Ejemplo|
|------------	|----------------------------------------------|---------------	|-----------	|
| *Nominal*    	| Uso de números en lugar de palabras 	| Identidad            	| Nacionalidad      	|
| *Ordinal*    	| Números se usan para ordenar series 	| + ranking            	| Nivel educacional 	|
| *Intervalar* 	| Intervalos iguales entre números    	| + igualdad           	| Temperatura       	|
| *Razón*      	| Cero real                           	| + aditividad         	| Distancia         	|
]

???

- Nominal: Números empleados como etiquetas (ej. sexo, raza)

- Ordinales: Distintas categorías puede sen ordenados en serie. Posición, no distancia. (ej. cargos en una empresa)

- Intervalares: Escalas de unidades iguales. Diferencia entre dos número consecuntivos refleja diferencia empírica. (ej. Horas del día)

- Razón: caracterizados por la presencia de un cero absoluto. (ej. frecuencias de eventos)

---
# Tablas de contingencia y asociación

----

.pull-left[
.content-box-red[
.center[
#¿Cómo establecer una medida de **asociación** de los datos en una tabla de contingencia?
]
]
]

.pull-right[
.content-box-purple[
.center[
#¿Cómo saber si esa asociación es **estadísticamente** significativa?
]
]
]
---
# Ejemplo (Datos CASEN 2022)

Pensemos en la siguiente pregunta de investigación:

**¿Existe una asociación entre la percepción de ser discriminado y el nivel educacional?**

`$H_a$`: el nivel educacional se asocia a la percepción de ser discriminado

`$H_0$`: no hay asociación entre nivel educacional y percepción de ser discriminado

---
## Tabla de frecuencias cruzadas

.pull-left-narrow[
.small[

``` r
pacman::p_load(sjPlot)
casen2022_chi %>%
  sjtab(educ_sup,
        discrim)
```
]]

.pull-right-wide[
.small[
<table style="border-collapse:collapse; border:none;">
 <tr>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a. ¿Cuál es el nivel educacional al que asiste o el más alto al cual asistió?</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">r9t. Últ. 12 meses: No ha sido tratado injustamente o discriminado</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th>
 </tr>
 
<tr>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">discriminad@</td>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">no discriminad@</td>
 </tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que universitaria</td>
<td style="padding:0.2cm; text-align:center; ">26996</td>
<td style="padding:0.2cm; text-align:center; ">141998</td>
<td style="padding:0.2cm; text-align:center; ">168994</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td>
<td style="padding:0.2cm; text-align:center; ">6476</td>
<td style="padding:0.2cm; text-align:center; ">26761</td>
<td style="padding:0.2cm; text-align:center; ">33237</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">33472</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">168759</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">202231</td> 
</tr>
<td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;2=247.461 &middot; df=1 &middot; &phi=0.035 &middot; p=0.000</td> 
</tr>
 
</table>
]]

---
.pull-left-narrow[

Con ambos porcentajes:
.small[

``` r
casen2022_chi %>%
  sjtab(educ_sup,
        discrim,
  show.row.prc=TRUE,
  show.col.prc=TRUE
  )
```
]]

.pull-right-wide[
.small[
<table style="border-collapse:collapse; border:none;">
 <tr>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a. ¿Cuál es el nivel educacional al que asiste o el más alto al cual asistió?</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">r9t. Últ. 12 meses: No ha sido tratado injustamente o discriminado</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th>
 </tr>
 
<tr>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">discriminad@</td>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">no discriminad@</td>
 </tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que universitaria</td>
<td style="padding:0.2cm; text-align:center; ">26996 16&nbsp;&#37; 80.7&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">141998 84&nbsp;&#37; 84.1&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">168994 100&nbsp;&#37; 83.6&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td>
<td style="padding:0.2cm; text-align:center; ">6476 19.5&nbsp;&#37; 19.3&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">26761 80.5&nbsp;&#37; 15.9&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">33237 100&nbsp;&#37; 16.4&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">33472 16.6&nbsp;&#37; 100&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">168759 83.4&nbsp;&#37; 100&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">202231 100&nbsp;&#37; 100&nbsp;&#37;</td> 
</tr>
<td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;2=247.461 &middot; df=1 &middot; &phi=0.035 &middot; p=0.000</td> 
</tr>
 
</table>
]
]

---

.pull-left-wide[
.small[
<table style="border-collapse:collapse; border:none;">
 <tr>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a. ¿Cuál es el nivel educacional al que asiste o el más alto al cual asistió?</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">r9t. Últ. 12 meses: No ha sido tratado injustamente o discriminado</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th>
 </tr>
 
<tr>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">discriminad@</td>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">no discriminad@</td>
 </tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que universitaria</td>
<td style="padding:0.2cm; text-align:center; ">26996 16&nbsp;&#37; 80.7&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">141998 84&nbsp;&#37; 84.1&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">168994 100&nbsp;&#37; 83.6&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td>
<td style="padding:0.2cm; text-align:center; ">6476 19.5&nbsp;&#37; 19.3&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">26761 80.5&nbsp;&#37; 15.9&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">33237 100&nbsp;&#37; 16.4&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">33472 16.6&nbsp;&#37; 100&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">168759 83.4&nbsp;&#37; 100&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">202231 100&nbsp;&#37; 100&nbsp;&#37;</td> 
</tr>
<td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;2=247.461 &middot; df=1 &middot; &phi=0.035 &middot; p=0.000</td> 
</tr>
 
</table>
]
]

.pull-right-narrow[
 
# ¿Cómo saber si existe asociación o no entre estas variables?
]

---
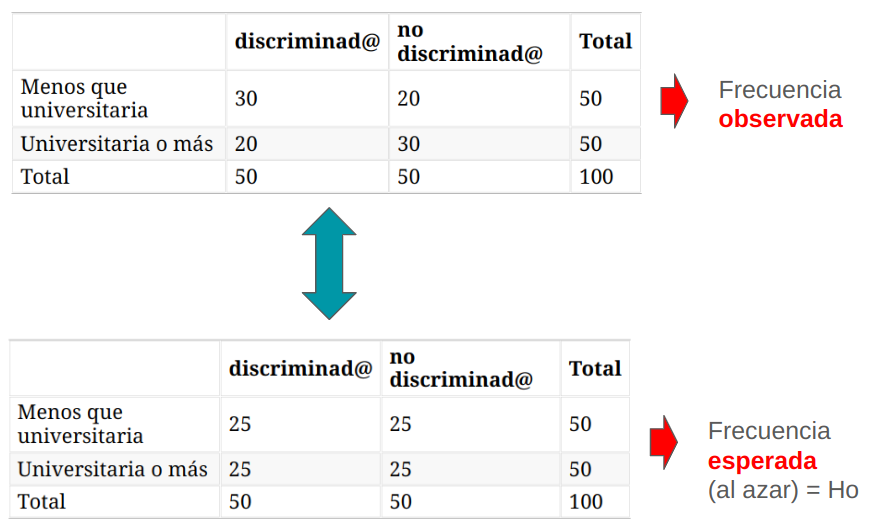
.medium[Para simplificar, pensemos en una muestra más pequeña de 100 casos. Pensemos que nuestra tabla (**observada**) es esta:] 
.small[
  
  |                         | discriminad@ | no discriminad@ | Total |
  |-------------------------|--------------|-----------------|-------|
  | Menos que universitaria | 30           | 20               | 50    |
  | Universitaria o más     | 20           | 30              | 50    |
  | Total                   | 50           | 50              | 100   |
  ]

.medium[Ahora veamos como sería una tabla **teórica** que exprese como sería una asociación total entre las variables: ]
.small[
  |                         | discriminad@ | no discriminad@ | Total |
  |-------------------------|--------------|-----------------|-------|
  | Menos que universitaria | 50           | 0               | 50    |
  | Universitaria o más     | 0            | 50              | 50    |
  | Total                   | 50           | 50              | 100   |
]

---
En lenguaje de test de hipótesis, la tabla **teórica** representa nuestra **hipótesis alternativa**:

- -> existe asociación entre percepción de discriminación y nivel educacional

--
.content-box-red[
Pero según la lógica de **falsación** de hipótesis, en lugar de analizar qué tan parecida es nuestra tabla observada a la tabla teórica de asociación, se contrasta la observada con una tabla donde **no hay asociación** 
]
--

La tabla de no-asociación es la **tabla de frecuencias esperadas al azar**

---
class: inverse middle center

## Una forma de generar evidencia de asociación bivariada en una tabla de contingencia es establecer si es **.yellow[distinta]** a una tabla sin asociación (frecuencia esperada al azar)

#-> .yellow[test de _diferencia_]

---
class: center 
.pull-left-wide[
![:scale 80%](img/lluvia.webp)
]

.pull-right-narrow[
 
# ¿Cómo sería una tabla sin asociación?

]
---

![:scale 95%](img/esperada-observada.png)

---
class: inverse middle

.pull-left[
.large[

# `$\chi^2$` 
]

(chi cuadrado)]

.pull-right[
El **.yellow[test de diferencia]** `$\chi^2$` (o simplemente chi cuadrado) consiste en  contrastar nuestra tabla de contingencia .yellow[observada] con una tabla donde no existe asociación entre variables (frecuencia .yellow[esperada] al azar), que representa la hipótesis nula `$H_0$`]

---
class: inverse middle center

La clave de esta prueba es el contraste tabla observada / tabla esperada al azar. Entonces:

# ¿Cómo obtener una tabla de frecuencias esperadas al azar?

---
## Frecuencia esperada al azar en una tabla de contingencia
----
.medium[
|                         | discriminad@ | no discriminad@ | Total |
|-------------------------|--------------|-----------------|-------|
| Menos que universitaria | a            | b               | (a+b) |
| Universitaria o más     | c            | d               | (c+d) |
| Total                   | (a+c)        | (b+d)           | N     |
]

ej: celda **a**, su frecuencia esperada es:

## `$$f_{e_{a}}=\frac{(a+b)(a+c)}{N}$$`

---
En base a los datos de nuestro ejemplo de 100 casos:
.small[
  
  |                         | discriminad@ | no discriminad@ | Total |
  |-------------------------|--------------|-----------------|-------|
  | Menos que universitaria | 30 .red[(a)] | 20 .red[(b)]    | 50    |
  | Universitaria o más     | 20 .red[(c)] | 30 .red[(d)]    | 50    |
  | Total                   | 50           | 50              | 100   |
  ]
`$$f_{e_{a}}=\frac{(a+b)(a+c)}{N}$$`
`$$f_{e_{a}}=\frac{(50)(50)}{100}= \frac{2500}{100}=25$$`

Por lo tanto, la frecuencia **esperada** al azar para la celda **a**=25

---
- Del ejemplo se podría deducir que la frecuencia esperada es simplemente el total de casos dividido por el número de celdas: 100/4=25.

- Esto ocurre en el ejemplo porque es una tabla **uniforme**: los totales de las filas y columnas son los mismos, por lo tanto la frecuencia esperada para cada celda es la misma

- ¿Qué pasa en una tabla **no uniforme**?

---
class: center 
![:scale 55%](img/lluvia2.webp)

---
.small[
|                         | discriminad@ | no discriminad@ | Total |
|-------------------------|--------------|-----------------|-------|
| Menos que universitaria | 40   (a)     | 20 (b)          |  60   |
| Universitaria o más     | 15   (c)     | 25 (d)          |  40   |
| Total                   | 55           | 45              | 100   |
]

En este caso, las frecuencias esperadas serán distintas para cada celda, ej:

`$$(a)=f_{e_{a}}=\frac{(a+b)(a+c)}{N}=\frac{60*55}{100}=\frac{3300}{100}=33$$`
`$$(b)=f_{e_{b}}=\frac{(a+b)(a+c)}{N}=\frac{60*45}{100}=\frac{2700}{100}=27$$`

---
# Pasos en el cálculo de `$\chi^2$`

- Generación de tabla de contingencia en base a nuestros datos -> tabla de **frecuencias observadas**

- Generación de tabla de contingencia **esperada** al azar en base a la tabla observada

- Establecer la diferencia entre lo **observado** y lo **esperado** al azar

- Establecer si esta diferencia es estadísticamente significativa

---
class: inverse middle right

.pull-left-narrow[
# Sentido general de la prueba de `$\chi^2$`
]

.pull-right-wide[
La lógica de la prueba de Chi 2 es la comparación de las frecuencias observadas `$(f_o)$` en nuestra tabla y de las frecuencias esperadas `$(f_e)$` por azar

----
Si nuestra tabla `$(f_o)$` se diferencia **significativamente** del azar `$(f_e)$`, entonces podemos rechazar la hipótesis nula y tenemos evidencia de asociación entre variables
]
---

.pull-left-narrow[
`$$f_{e_{a}}=\frac{(a+b)(a+c)}{N}$$`
`$$f_{e_{b}}=\frac{(a+b)(b+d)}{N}$$`
`$$f_{e_{c}}=\frac{(a+c)(c+d)}{N}$$`
`$$f_{e_{d}}=\frac{(b+d)(c+d)}{N}$$`
]
.pull-right-wide[
.small[
|                         | discriminad@ | no discriminad@ | Total |
|-------------------------|--------------|-----------------|-------|
| Menos que universitaria | a            | b               | (a+b) |
| Universitaria o más     | c            | d               | (c+d) |
| Total                   | (a+c)        | (b+d)           | N     |
]

## `$$\chi^2=\sum\frac{(f_o-f_e)^2}{f_e}$$`

El valor de Chi2  será mayor en la medida que lo observado sea distinto de los esperado al azar

]

---
Cálculo de frecuencias esperadas para ejemplo con CASEN

.pull-left[
.small[
<table style="border-collapse:collapse; border:none;">
 <tr>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a. ¿Cuál es el nivel educacional al que asiste o el más alto al cual asistió?</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">r9t. Últ. 12 meses: No ha sido tratado injustamente o discriminado</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th>
 </tr>
 
<tr>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">discriminad@</td>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">no discriminad@</td>
 </tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que universitaria</td>
<td style="padding:0.2cm; text-align:center; ">26996</td>
<td style="padding:0.2cm; text-align:center; ">141998</td>
<td style="padding:0.2cm; text-align:center; ">168994</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td>
<td style="padding:0.2cm; text-align:center; ">6476</td>
<td style="padding:0.2cm; text-align:center; ">26761</td>
<td style="padding:0.2cm; text-align:center; ">33237</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">33472</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">168759</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">202231</td> 
</tr>
<td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;2=247.461 &middot; df=1 &middot; &phi=0.035 &middot; p=0.000</td> 
</tr>
 
</table>
]
]

.pull-right[
.small[
`$$f_{e_{a}}=\frac{168994*33472}{202231}=27970.8$$`
`$$f_{e_{b}}=\frac{168994*168759}{202231}=141023.2$$`
`$$f_{e_{c}}=\frac{33472*33237}{202231}=5501.2$$`
`$$f_{e_{d}}=\frac{168759*33237}{202231}=27735.8$$`
]
]

---
En R también es posible obtener las frecuencias esperadas por celda con la función `CrossTable` de la librería `gmodels`

``` r
gmodels::CrossTable(casen2022_chi$educ_sup,
                    casen2022_chi$discrim, 
                    expected=TRUE,
                    prop.r = FALSE, 
                    prop.c=FALSE, 
                    prop.chisq = FALSE, 
                    prop.t = FALSE)
```

---
.small[

```
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |              Expected N |
## |-------------------------|
## 
##  
## Total Observations in Table:  202231 
## 
##  
##                        | casen2022_chi$discrim 
## casen2022_chi$educ_sup |         0 |         1 | Row Total | 
## -----------------------|-----------|-----------|-----------|
##                      0 |     26996 |    141998 |    168994 | 
##                        | 27970.821 | 141023.179 |           | 
## -----------------------|-----------|-----------|-----------|
##                      1 |      6476 |     26761 |     33237 | 
##                        |  5501.179 | 27735.821 |           | 
## -----------------------|-----------|-----------|-----------|
##           Column Total |     33472 |    168759 |    202231 | 
## -----------------------|-----------|-----------|-----------|
## 
##  
## Statistics for All Table Factors
## 
## 
## Pearson's Chi-squared test 
## ------------------------------------------------------------
## Chi^2 =  247.7146     d.f. =  1     p =  8.178928e-56 
## 
## Pearson's Chi-squared test with Yates' continuity correction 
## ------------------------------------------------------------
## Chi^2 =  247.4605     d.f. =  1     p =  9.291443e-56 
## 
## 
```
]

---
.small[
`\begin{align*}
\chi^2&=\sum\frac{(f_o-f_e)^2}{f_e} \\ \\
&=\frac{(26996-27970.8)^2}{27970.8}+\frac{(141998-141023.2)^2}{141023.2}+\frac{(6476-5501.2)^2}{5501.2}+ \frac{(26761-27735.8)^2}{27735.8} \\\\
&=\frac{(974.8)^2}{27970.8}+\frac{(974,8)^2}{141023.2}+\frac{(-974.8)^2}{5501.2}+ \frac{(-974.8)^2}{27735.8} \\\\
&=\frac{950235,04}{27970.8}+\frac{950235,04}{141023.2}+\frac{950235,04}{5501.2}+ \frac{950235,04}{27735.8} \\\\
&=33.97+6.74+172.7+34.3 \\\\
\end{align*}`
]

# `$$\chi^2=247.46$$`

---
# Inferencia y `$\chi^2$`

- Tal como en los pasos de la inferencia para pruebas anteriores (como `$Z$` y `$t$`), para realizar la prueba de hipótesis comparamos el valor observado de `$\chi^2$` con un valor crítico, que proviene de la distribución `$\chi^2$`

- además de especificar la probabilidad de error  `$\alpha$`, se requiere especificar los **grados de libertad**

---
# Grados de libertad en `$\chi^2$`

- Como en la distribución `$t$`, `$\chi^2$` también se ajusta por los grados de libertad, que se obtienen sumando el numero de niveles/categorías -1 de cada variable

- En nuestro ejemplo de tabla de 2x2 (dos categorías de cada variable), los grados de libertad equivalen a:

`$$gl=(2-1)*(2-1)=1*1=1$$`

---

![](img/chi_dist2.png)

---
# Comparación  valor crítico y valor estimado

- `$\chi^2$` estimado: **247.46**

- `$\chi^2$` crítico para un `$\alpha=0.05$` y 1 grado de libertad: **3.84**

- En el ejemplo: **valor estimado `$\chi^2$` > valor crítico `$\chi^2$`**

- Por lo tanto **se rechaza `$H_0$`**, podemos decir que hay evidencia de asociación entre percepción de discriminación y nivel educacional con un 95% de confianza

---
# `$\chi^2$` directamente en R

La función es  `chisq.test()`

``` r
chisq.test(table(casen2022_chi$educ_sup,
                 casen2022_chi$discrim))
```

```
## 
## 	Pearson's Chi-squared test with Yates' continuity correction
## 
## data: table(casen2022_chi$educ_sup, casen2022_chi$discrim)
## X-squared = 247.46, df = 1, p-value < 2.2e-16
```

---

.pull-left-narrow[
.medium[
De todas maneras, aparece directamente en varios outputs de tablas de contingencia en R, como la generada antes con `sjtab`, de librería `sjPlot`:

``` r
casen2022_chi %>%
  sjtab(educ_sup,
        discrim,
  show.row.prc=TRUE)
```
]
]

.pull-right-wide[
 
.small[
<table style="border-collapse:collapse; border:none;">
 <tr>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a. ¿Cuál es el nivel educacional al que asiste o el más alto al cual asistió?</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">r9t. Últ. 12 meses: No ha sido tratado injustamente o discriminado</th>
 <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th>
 </tr>
 
<tr>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">discriminad@</td>
 <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">no discriminad@</td>
 </tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que universitaria</td>
<td style="padding:0.2cm; text-align:center; ">26996 16&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">141998 84&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">168994 100&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td>
<td style="padding:0.2cm; text-align:center; ">6476 19.5&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">26761 80.5&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; ">33237 100&nbsp;&#37;</td> 
</tr>
 
<tr> 
<td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">33472 16.6&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">168759 83.4&nbsp;&#37;</td>
<td style="padding:0.2cm; text-align:center; border-bottom:double;">202231 100&nbsp;&#37;</td> 
</tr>
<td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;2=247.461 &middot; df=1 &middot; &phi=0.035 &middot; p=0.000</td> 
</tr>
 
</table>
]
]

---
# Resumen: 5 pasos inferencia para tablas cruzadas

1. Establecer las hipótesis

2. Calcular frecuencias esperadas

3. Estimar estadístico de prueba `$\chi^2$`

4. Establecer valor crítico de la prueba (de acuerdo a un cierto nivel de confianza y grados de libertad)

5. Contraste e interpretación

---
class: inverse bottom right

# Tamaños de efecto de asociación en tablas de contingencia

---
# Coeficiente Phi

- El Coeficiente Phi (φ) es una medida de asociación entre dos variables binarias.

- Es similar al coeficiente de correlación de Pearson pero específico para una tabla de contingencia de  2x2.

- Se interpreta de la misma manera que Pearson en términos de sentido (positivo/negativo) y fuerza (cercanía a 1 / -1)

---
.small[
  
  |                         | discriminad@ | no discriminad@ | Total |
  |-------------------------|--------------|-----------------|-------|
  | Menos que universitaria | 30 .red[(a)] | 20 .red[(b)]    | 50    |
  | Universitaria o más     | 20 .red[(c)] | 30 .red[(d)]    | 50    |
  | Total                   | 50           | 50              | 100   |
  ]

`\begin{align*}
  \phi &= \frac{ad - bc}{\sqrt{(a + b)(c + d)(a + c)(b + d)}} \\
  &= \frac{(30 \times 30) - (20 \times 20)}{\sqrt{(30 + 20)(20 + 30)(30 + 20)(20 + 30)}} \\
  &= \frac{900 - 400}{\sqrt{6250000}} \\
  &= \frac{500}{2500} \\
  &= 0.2
\end{align*}`

---

.pull-left-wide[

``` r
tabla <- matrix(c(30, 20, 20, 30), 
 nrow = 2, byrow = TRUE)
print(tabla)
```

```
##      [,1] [,2]
## [1,]   30   20
## [2,]   20   30
```

``` r
coef_phi <-psych::phi(tabla)
print(coef_phi)
```

```
## [1] 0.2
```
]

.pull-right-narrow[
 
 
 
 
 
 
 
 
 El valor de 0.2 indica una asociación baja entre ambas variables de la tabla de contingencia

]

---
# V de Cramer

Es una medida general de asociación para tablas que pueden ir más allá de 2x2:

## `$V_{Cramer}=\sqrt{\frac{\chi²}{n * (k - 1)}}$`

Donde:

- χ² es el valor del estadístico Chi-cuadrado.
- n es el total de observaciones.
- k es el menor número entre las filas o columnas de la tabla.

---
| Grupo  | Categoría 1 | Categoría 2 |
|--------|-------------|-------------|
| A      |     30      |     20      |
| B      |     10      |     40      |
| C      |     50      |     30      |

- χ² = 5.35
- n = 180
- La tabla es 3x2, por lo que k = 2.

`$V = \sqrt{\frac{5.35} {180 * (2 - 1)}}=\sqrt{\frac{5.35}{180}}=0.173$`

Por lo tanto, existe una asociación débil entre las variables

---
---
# Medidas de asociación según nivel de medición
----

.small[

|                       | **Nominal Dicotómica**      | **Nominal Politómica**      | **Ordinal**                 | **Intervalar/Razón**       |
|-----------------------|----------------------------|----------------------------|----------------------------|---------------------------|
| **Nominal Dicotómica**|       Tetracórica / Chi2     |                |                             |    |
| **Nominal Politómica**|         Chi2       |    Chi2             |       |                             |
| **Ordinal**           |     Biserial       |  Chi2                          | Spearman, Kendall           |                 |
| **Intervalar/Razón**  | Punto Biserial / Prueba t   |  (ANOVA)                          | Pearson/biserial, Policórica                 | Pearson       |

]

---
class: front

.pull-left-wide[
# Estadística Correlacional]

.pull-right-narrow[![:scale 85%](img/logo-correlacional-transp.png)]

## Inferencia, Asociación y reporte

----
.pull-left[

## Juan Carlos Castillo
## Sociología FACSO - UChile
## 2do Sem 2024
## [.orange[correlacional.netlify.com]](https://encuestas-sociales.netlify.com)
]